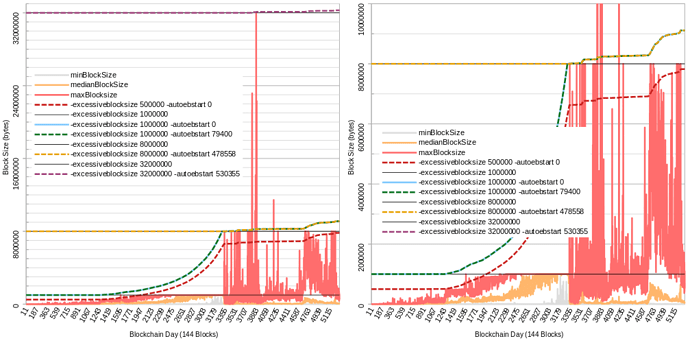
I removed the part where it would introduce a new rule. It’s the same EB, but adjusted upwards by those who’d decide to stick to the algo. Those running with EB=32 and those with EB=32+algo would be compatible for as long as majority of hashpower doesn’t produce a block of >32MB and <(32+algo_bonus). If a >32MB chain would dominate, then those running with EB32 could either bump it up manually to some EB64 and have peace until algo catches up to 64, or just snap to algo too.
changes in such probably should follow established capacity of widely used infrastructure. So the BCHN node currently ships with EB=32MB because we know it can handle that. When that moves to 50MB or 64MB at some time in the future, again based purely on the software being able to handle that, your algorithm may become more agressive.
You can make this internally consistent for it to simply respond to the user-set EB, which for most is the software-default EB.
If need be, a faster increase could be accommodated ahead of being driven by the algo, by changing the EB config so nodes would then enforce EB64(+algo_bonus). It wouldn’t make the algo more aggressive - it would just mean it will not do anything until mined blocks start hitting the treshold_size=EB/HEADROOM_FACTOR.
Any changes to the algo have nothing to do with the yearly protocol upgrades.
I see what you mean, but IMO it’s more convenient to snap the change in EB to protocol upgrades, to have just 1 “coordination event” instead of 2 and avoid accidentally starting reorg games.
Mining software can suddenly start selecting transactions based on reaching a certain amount of fees income.
Miners are really the customer of this and features are enabled based on merit. Does this increase the paycheck of the miner.
It would be nice to suggest some good (optional) policy for mined block size, one such that would maximize revenue and minimize orphan risks and account for the miner-specific capabilities, risk-tolerance, and connectivity. Right now it seems like it’s mostly flat 8MB, and no miner bothered to implement some algo by himself even though nothing is preventing him from doing so.
In the meantime I had a few other discussions that might be of interest:
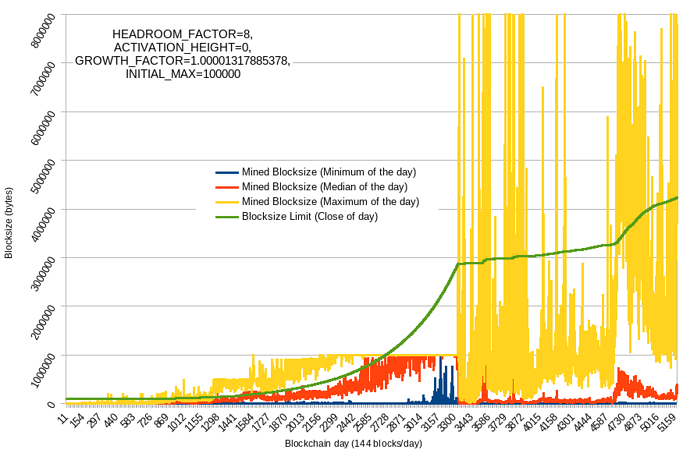
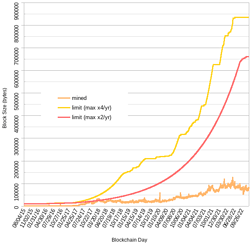
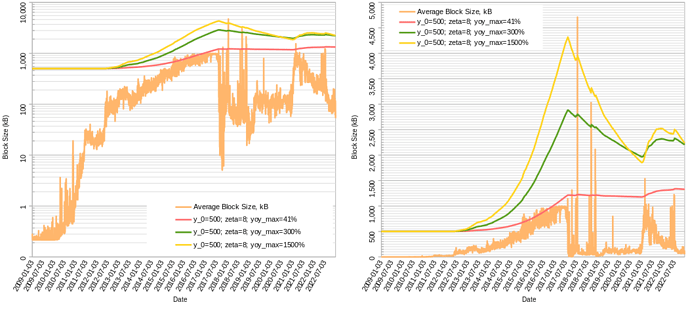
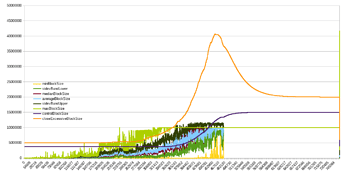
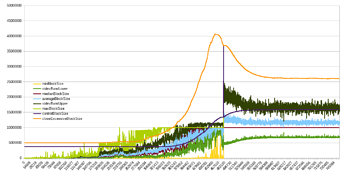
Some backtesting against Ethereum (left - linear scale, right - log scale) in trying to understand whether headroom (target “empty” blockspace, set to 87.5%) is sufficient to absorb rapid waves of adoption without actually hitting the limit:
The red line is too slow, it doesn’t reach the target headroom till the recent bear market.
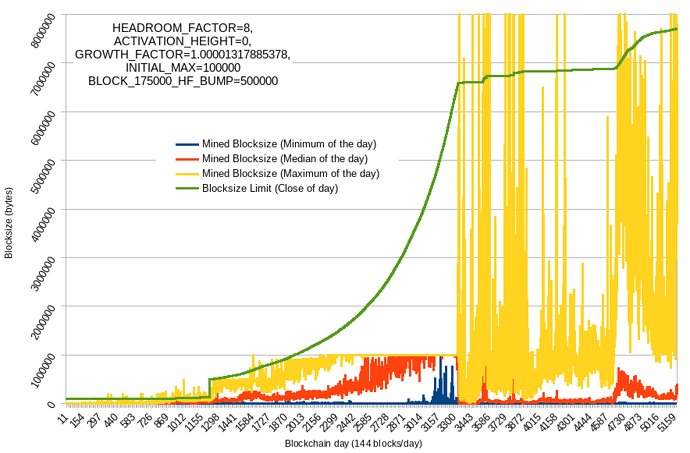
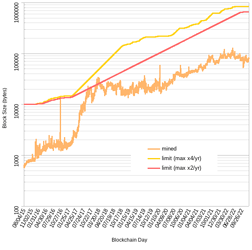
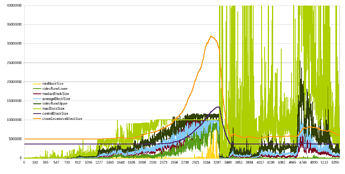
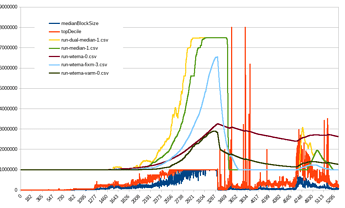
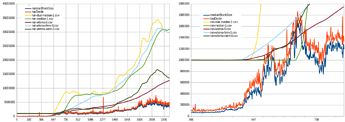
Here’s some more back-testing against BTC+BCH, assuming the algo was activated at same height as the 1MB limit (red- max speed 4x/yr, orange- 2x/yr):
It wouldn’t get us to 32MB today (due to blocks in dataset all below 1MB until '17, otherwise it actually could have) but it would have gotten us to 8MB in 2016 even with mined blocks <1MB !!
The thing I really like is it “saving” our progress. If there was enough activity and network capacity in the past, then can we assume capacity is still there and that activity could come rushing back at any moment? See how it just picks up where it left off in beginning of 2022 and continues growing from there, even if median blocksize was below <1MB because the frequency of blocks above threshold (1MB for EB8) was enough to start pushing the EB up again (at a rate slower than max, though). The algo limit would only cut off those few test blocks (I think only 57 blocks bigger than 8MB).
New CHIP
I believe this approach can be “steel-manned” and to that end I have started drafting a CHIP, here below is a 1-pager technical description, would appreciate any feedback - is it clear enough? I’ll create a new topic soon, any suggestions for the title? I’m thinking CHIP-2022-12 Automated Excessive Blocksize (AEB)
Some other sections I think would be useful:
- Rationale
- Choice of algo - jtoomim’s and my arguments above in this thread
- Choice of constants (tl;dr I got 4x/yr as max speed from backtesting, target headroom- similar rationale as @im_uname 's above, and the combo seems to do well tested against historical waves of adoption)
- Backtesting
- Bitcoin 2009-2017 (1mb + algo)
- BCH 2019-now (1mb + algo)
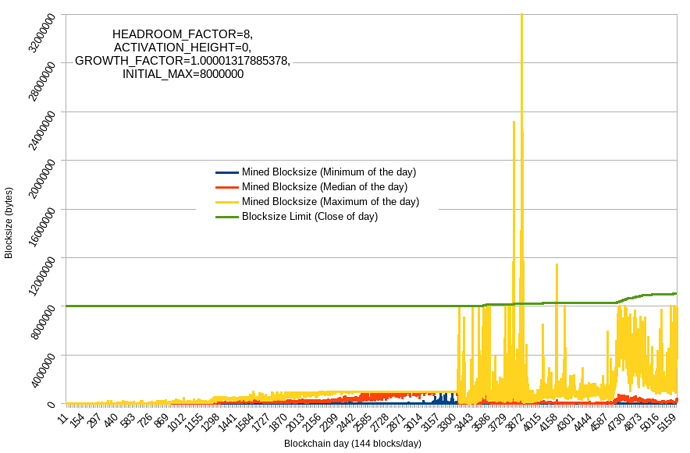
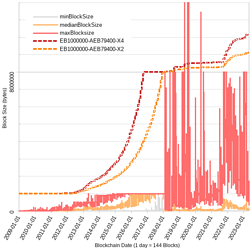
- BTC+BCH full history flatEB VS autoEB, with eb config changes to match historical EB changes (0, 0.5mb, 1mb, 8mb, 32mb)
- Ethereum
- Cardano?
- Specification - separated from math description because we need to define exact calculation method using integer ops so it can be reproduced to the bit
- Attack scenarios & cost of growth
Technical Description
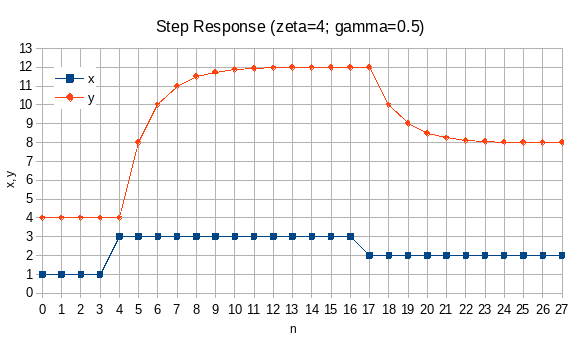
The proposed algorithm can be described as intermittent exponential growth.
Exponential growth means that excessive block size (EBS) limit for the next block will be obtained by multiplying a constant growth factor with the current block’s EBS.
Intermittent means that growth will simply be skipped for some blocks i.e. EBS will carry over without growing.
The condition for growth will be block utilization: whenever a mined block is sufficiently full then EBS for the next block will grow by a small and constant factor, else it will remain the same.
To decide whether a block is sufficiently full, we will define a threshold block size as EBS divided by a constant HEADROOM_FACTOR.
The figure below illustrates the proposed algorithm.
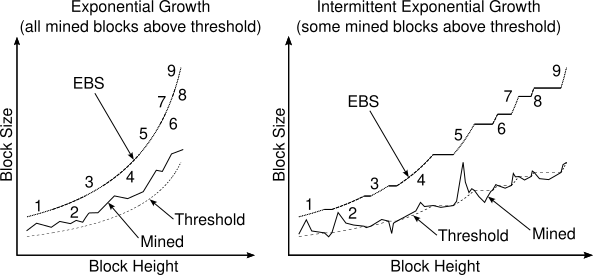
If current blockchain height is n then EBS for the next block n+1 will be given by:
excessiveblocksize_next(n) = excessiveblocksize_0 * power(GROWTH_FACTOR, count_utilized(ANCHOR_BLOCK, n, HEADROOM_FACTOR))
where:
-
excessiveblocksize_0 - configured flat limit (default 32MB) for blocks before and including AEBS_ANCHOR_HEIGHT;
-
GROWTH_FACTOR - constant chosen such that maximum rate of increase (continuous exponential growth scenario) will be limited to +300% per year (52595 blocks);
-
count_utilized - an aggregate function, counting the number of times the threshold block size was exceeded in the specified interval;
-
AEBS_ANCHOR_HEIGHT is the last block which will be limited by the flat excessiveblocksize_0 limit;
-
HEADROOM_FACTOR - constant 8, to provide ample room for short bursts in blockchain activity.