I have created an FAQ regarding quantum computing at: What about quantum computing? Are my BCH safe? | The Bitcoin Cash Podcast
I’ll give you some more things to consider.
How to add support for some post-quantum signature scheme?
That’s relatively easy, it’s a drop-in, we can extend OP_CHECKSIG[VERIFY], OP_CHECKMULTISIG[VERIFY], and OP_CHECKSIG[VERIFY] just like we did when we added support for Schnorr signatures and Schnorr multisig: the opcode reads the length of pushed signature and from that determines how to interpret it and which method to use to validate.
With post-quantum crypto, keys & signatures would be bigger so same method is usable there: opcode can internally switch what scheme it uses based on the length of arguments.
Addresses would stay the same, UTXO size would stay the same, however input sizes would grow since they’d have to reveal bigger pubkeys and signatures, lowering the network’s TPS per megabyte of block size. See here for more info.
How to migrate from safe-at-rest elliptic curve P2PKH to post-quantum P2PKH
If quantum computers would become fast enough, adversary could intercept your transaction, discover your public key, and attempt to generate an alternative signature and replace your TX with his.
If that was a real threat, a new consensus rule could require and intermediate step for transferring funds from such UTXOs, a commit-delay-reveal scheme:
While your pubkey is still secret, you’d create a TX, hash it, then publish the hash on the chain. After the hash has been embedded to a safe depth, you’d publish the TX and reference the hash.
The adversary could generate an alternative TX, but he could not have an aged hash ready, and by the time he makes one, your TX will have been mined.
The paper linked above describes the method for migration in detail:
Can I store BCH in a quantum-safe address today?
Nice thing about Bitcoin Cash having powerful scripting capabilities is that it’s already possible to lock up funds in a quantum-safe contract (P2SH32), one that requires an aged pre-commitment + signature.
I outlined it in the P2SH bulletin at the end of section 5.
Are 160-bit P2PKH addresses that DID NOT reveal their pubkey vulnerable?
Theoretically yes, practically no. Grover’s algorithm could find an alternative spending key in a finite amount of time BUT:
Assuming a clock speed on scale of GHz, this would take about 10 million years. Important to note is that splitting the work and doing it in parallel is not as beneficial as with classic computers because it would offer only a quadratic speedup (Fluhrer, S., Reassessing Grover’s Algorithm). In other words, doing the work in 1 year would require building 100 trillion quantum computers because
sqrt(100T) == 10M. Therefore, we can say that breaking a 160-bit hash preimage is physically possible because 10M years is a finite amount of time and less than age of the universe. However, it is still infeasible.
What about abandoned coins with pubkeys revealed?
They’d be free for the taking because original owners wouldn’t act during the window of opportunity to move the coins to quantum-resistant storage and so they’re as good as gone as soon as Shor’s algorithm becomes feasible. I guess it can be considered a bounty for the first to implement Shor’s 
Without necessarily responding to prior comments, a big question would be how would BCH transition from one algorithm to another, with the dependence on ASICs at some point in the future?
Could a transition algorithm be used… with inspiration taken from the Storm proposal way back when. Take a similar idea, where current SHA-256 ASICs mine weak blocks, and whatever the new algorithm is, and computers that compute it, mine strong blocks. And over time strong blocks will be the only ones mined.
A transitioning of an algorithm will be a challenge. And I highly doubt there will be any algorithm that current ASICs can run that will be resistant to QC.
Is there another method to this that would work? Such as a PoS approach? I’m not a fan of PoS for a multitude of reasons, so I don’t see this as an option.
Out of curiosity, would Avalanche (BCHABC concept from a while back, of which I think they finally began to implement) provide some protection from QC? Or could an idea like that be modified to protect from QC?
Got one more link to add:
I found something: Delgado Segura, Sergi & Pérez-Solà, Cristina & Navarro-Arribas, Guillermo & Herrera-Joancomartí, Jordi. (2018). Analysis of the Bitcoin UTXO set.
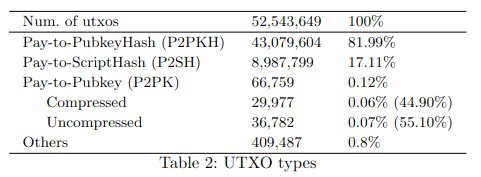
They didn’t analyze how many of P2PKH UTXOs had their public key revealed.
We won’t need to. Quantum Computers won’t break our PoW. The only thing that’s at risk is the signature scheme (based on ECC - elliptic curve cryptography), nothing else.
That is interesting, though they also don’t show value stored. The percentages are utxos rather than value stored in each type. It still gives an approximate value though.
Yup. I want to know the value, too, I have it on my todo to build a little program that can pull the data and process it so we can answer this Q, can’t promise anything but in next couple of months I think I could deliver something.
In the meantime, I built a proof-of-concept for this, here: Quantum-resistant One-time-use Lock
I hope that in '25 we’ll be activating CHIP 2021-05 Targeted Virtual Machine Limits
With 10k stack item limit and removal of opcode count, Lamport implementation could fit in a single input. Quoting Moonsetler on X:
i think you could do a variant of lamport specifically altered to fit bch script better, that is about 4kb (plus change) and fits into the ops limit.
Lamport requires use of one-time keys, so using the contract’s address for receiving payments would be risky because there’s no way to really ensure people will not pay into it after it has been used.
However, thanks to CashTokens, we can work around that and have a constant receiving address - one that requires a particular NFT (held by a Lamport locking bytecode) to be spent as sibling:
<0> OP_UTXOTOKENCATEGORY
<16> OP_SPLIT OP_DROP
<half_of_your_NFT_categoryID> OP_EQUAL
Then only the owner would need to interact with the Lamport contract, for when he wants to spend from the pay-to-token address, and he could rotate the key on every spend.
According to Pierre-Luc (CEO of Pauli group, focused on QC-hardening on Ethereum), by the end of this decade we could see ECC get broken:
The sweetspot is to aim at machines that can break keys in hours/days at first. It takes more error correction (i.e. more physical qubits overhead) for a calculation to last a whole year. The number of step is fixed (~10^8) and going slow doesn’t necessarily helps with resources.
Everyone is aiming at machines that can to about this number of steps by the end of the decade. Then there is still some distance to the machines that can do 10^12 operations to break RSA 2-3 years afterward.
If we’ll be able to implement Lamport in Script, then we could secure our wealth until we find something better, quoting Pierre-Luc again (responding to my idea of Lamport + pay-to-token):
Excellent, if the largest addresses add Lamport then already that’s most of the attack surface covered.
Yeah it makes sense to keep one address.
The BitVM folks are using the stateful to create state machine also it seems, there are a few neat tricks to play with hash based signatures.
Another thing that would be interesting would be how many have their public key exposed.
If you ever do the parser, it would be good to have something like:
P2PKH-secret: 20%
P2PKH-revealed: 80%
That would be more complex to parse though. You would have to create a record of all revealed keys first. This would also apply to P2SH.
Also, some may be revealed but never included in the blockchain.
Another question is how secure Armory outputs are. Even without re-use they may be breakable due to how they are generated.
I parsed the blockchain up until block 872000 and got the data on value:
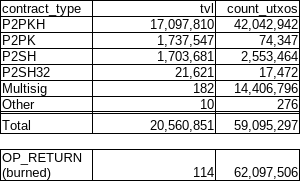
That’s great. I assume tvl is total value?
P2PKH overwhelms the others by value.
So, most of the coins would be potentially protected against quantum computers. The exceptions would be for ones that have key re-use.
Even normal P2SH (160) would be moderately protected at 80-bit security. They would have lower than 128-bit security, but would be effort to break them one at a time.
The only ones that are definately exposed would be the P2PK. They are likely mostly old and maybe private keys are lost.
Hopefully quantum computers won’t suddenly jump to be able to create cryptographic keys instantly. If people have notice, it is likely almost everything (where the private key isn’t lost) could be protected.
Yes
Yes, and if keys are exposed it likely means the keys are not lost. So, if need be, they could be moved to non-exposed P2PKH.
I’ll see if I can extract the exposed vs non-exposed info, too.
More than “moderately”. I was wondering about post-quantum preimage resistance of HASH160 addresses (both P2PKH and P2SH), too. Turns out, it would be physically possible but still infeasible to crack even 1 address:
We could design a black box function to break both P2PKH and P2SH (and P2WSH, etc.) addresses in 2^80 single-threaded quantum computer cycles.
Assuming a clock speed on scale of GHz, this would take about 10 million years.
Important to note is that splitting the work and doing it in parallel is not as beneficial as with classic computers because it would offer only a quadratic speedup (Fluhrer, S., Reassessing Grover’s Algorithm).
In other words, doing the work in 1 year would require building 100 trillion quantum computers becausesqrt(100T) == 10M.
Therefore, we can say that breaking a 160-bit hash preimage is physically possible because 10M years is a finite amount of time and less than age of the universe.
However, it is still infeasible.
.
Some old keys have been recently observed moving on BTC, but still, Satoshi’s P2PK stash didn’t move, and it is still the biggest quantum-computing bounty in the world.
Yeah. There isn’t much that can be really done about it.
Anyone who knows what their keys would likely have time before the break is possible.
Once/If quantum computers can trivially break the outputs, it would be impossible to distinguish the original owner from someone with a QC. It isn’t clear why anyone should get those outputs.
Before that it would be worth looking into having a system to handle hash protected outputs.
It would probably be some kind of on-chain two stage release system. Submit the digest of the insecure public key and one that works with a new algorithm. Once it is buried, the new public key can be used to spend the funds.
Sounds like a commit-delay-reveal scheme, I first saw it described here: Stewart, I., et. al. (2018). “Committing to quantum resistance: A slow defence for Bitcoin against a fast quantum computing attack”
On BCH, we can implement that as a smart-contract, here’s the proof-of-concept: Quantum-resistant One-time-use Lock
I assume that requires moving all P2SH outputs to new outputs (with the smart contract) manually first to protect them?
In that case, they could just be moved to quantum resistant outputs.
If a quantum computer was suddenly able to break the elliptic curve signature algorithm, then there would need to be a soft fork to force all P2SH outputs to additionally require a commit transaction.
After the soft fork, you have to send the commit first because P2SH outputs would require the normal signature and a reference to a commit transaction.
Edit:
Also, it would be a good idea if it could handle pre-signed transactions. If someone had a valid transaction in a safe, then the client would take that transaction and produce a valid commit transaction for sending.
Really good talk from the BTC guys at OP_NEXT. I’ll need to watch this again, but for me the key points really were that the government is looking to be quantum secure 2030 - 2033, and somewhere in the range of 2026 to 2030 is probably ideal for Bitcoin.
This means if we’ve already locked in 2025 that we do need to get this onto the radar so that we can ship BCH quantum resistance changes 2026 - 2028 sometime.
It’s also a point of community discussion as to the economic effect. For instance, is there a case to hard fork in a “burn” of all Satoshi + other vulnerable coins after an announced window to move to quantum secure? Or do we let a huge amount of value in the UTXO set get grabbed by quantum computers?
The 2025 VM Limits upgrade may also help us out significantly I guess in terms of opening the ability for more cryptographic defenses.
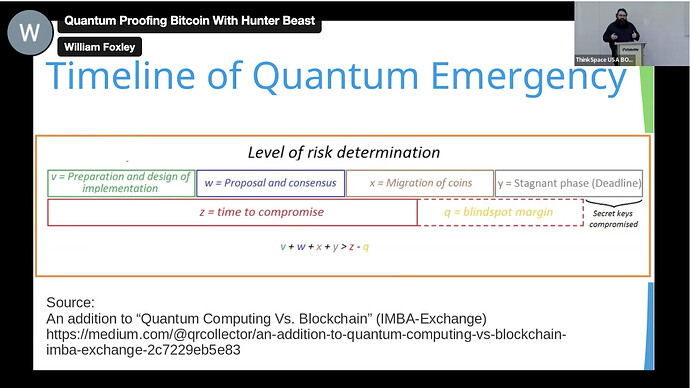
See this graph of how you need to prep & migrate coins (with some margin for error) BEFORE the attack becomes viable obviously.
Government timeline:
The PoC smart contract is only good for someone who’d want to preemtively move his funds to a quantum-resistant address. Once QCs become available, you’d want a fork to enable safely migrating funds from any stranded and vulnerable contracts (including any non-standard variations of P2PKH, P2PKH, P2SH) where a commit-delay-reveal could work to prove original ownership.
Caveat with commit-delay-reveal is that miners could collude to steal, making a 51% potentially more damaging (right now, 51% could only censor transactions, or execute a double-spend fraud, but not out-right steal someone else’s funds) but once signatures are broken there’s no way around it but to use your P2PKH / P2SH address as an aged hashlock. With a long enough aging requirement, I think this would not be a deal-breaker.
I don’t consider P2SH or P2PKH preimage to be breakable, so consideration here is just vulnerability of redeem scripts, where they’d become vulnerable only after exposing a vulnerable redeem script, same how P2PKH becomes vulnerable only after exposing the committed key.
With P2SH, it is more complex, because some contracts may already be quantum-resistant (signatureless covenants etc.), and only some would be vulnerable to QCs. Having a SF to require a commit for all of P2SH could inconvenience non-vulnerable contracts or could even break them (if contract requires a particular number of inputs & outputs and commitment would be provided by an additional input or output).
Therefore, I think a complete solution would be to extend the TX format so that this commit-delay-reveal happens “outside” the legacy TX, so that it doesn’t interfere with functioning of existing contracts and it would only be required for any script that executes OP_CHECKSIG, CHECKDATASIG, or CHECKMULTISIG with elliptic curve keys.
BTC Core has a speculative PR for Quantum resistant addresses as a soft fork: QuBit - P2QRH spending rules by cryptoquick · Pull Request #1670 · bitcoin/bips · GitHub
Of course it’s overengineered, yet another level of segregating the witness.
But anyway, nice doc, here’s the link to view the doc: https://github.com/bitcoin/bips/blob/e186b52cff5344c789bc5996de86697e62244323/bip-p2qrh.mediawiki
smells like FUD, and conveniently there’s a bunch of new coins claiming quantum resistance