(post deleted by author)
I’m making a small but important tweak to the algo, changing:
- εn = max(εn-1 + γ ⋅ (ζ ⋅ min(xn-1, εn-1) - εn-1), ε0) , if n > n0
to:
-
εn = εn-1 + (ζ - 1) / (αn-1 ⋅ ζ - 1) ⋅ γ ⋅ (ζ ⋅ xn-1 - εn-1) , if n > n0 and ζ ⋅ xn-1 > εn-1
-
εn = max(εn-1 + γ ⋅ (ζ ⋅ xn-1 - εn-1), ε0) , if n > n0 and ζ ⋅ xn-1 ≤ εn-1
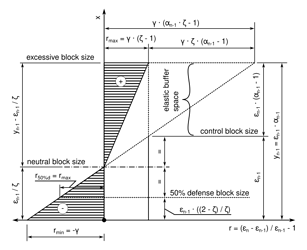
This means that response to block size over the threshold will adjust smoothly up until the max. instead of having max. response to any size between εn-1 (“control block size”) and yn-1 (“excessive block size”).
The per-block response is illustrated with the figures below.
Old version:
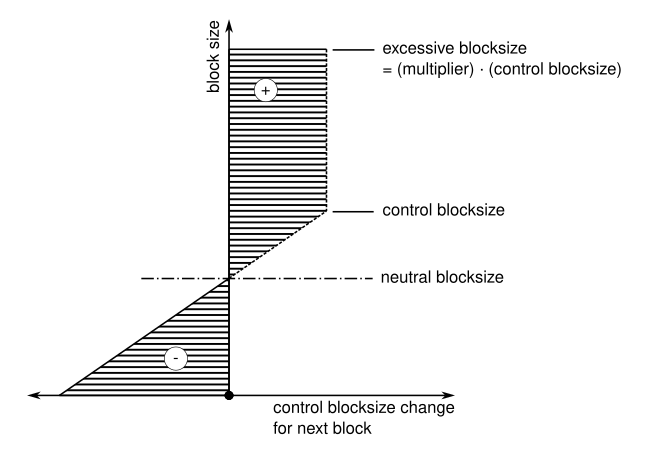
New version:
In other words, instead of having the response clipped (using the min() function), we now scale it down proportional to the multiplier increase so it always takes 100% full blocks to get max. growth rate, as opposed to previous version, where any size above control block size would trigger max. response.
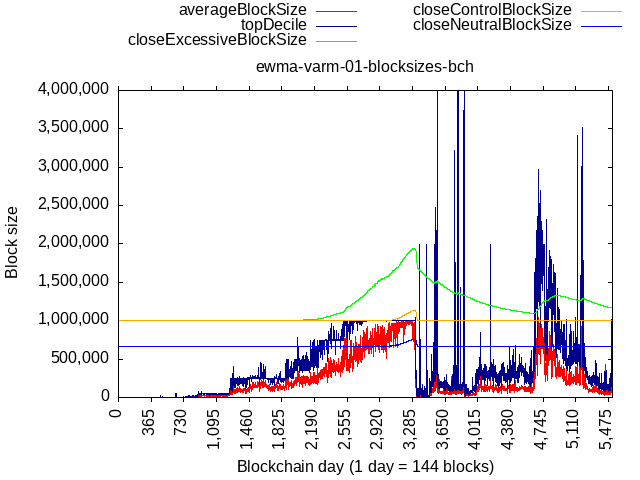
Back-testing:
- BCH
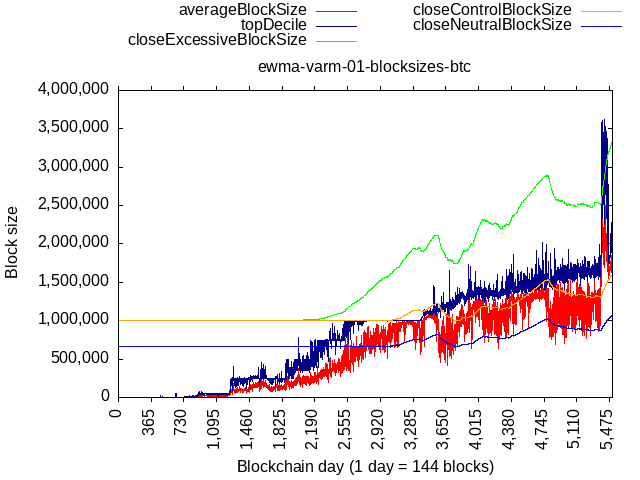
- BTC
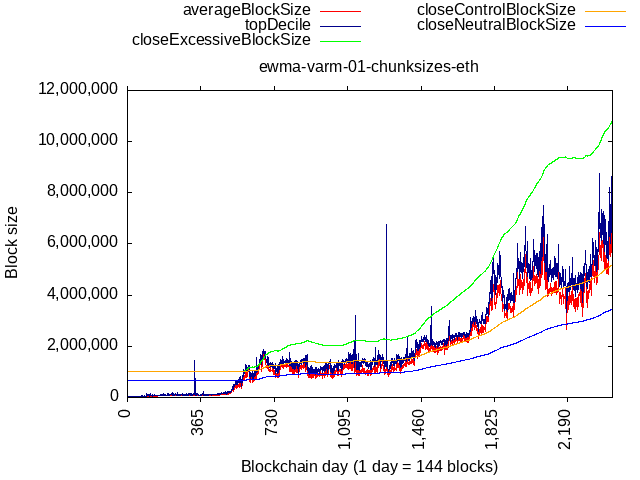
- ETH
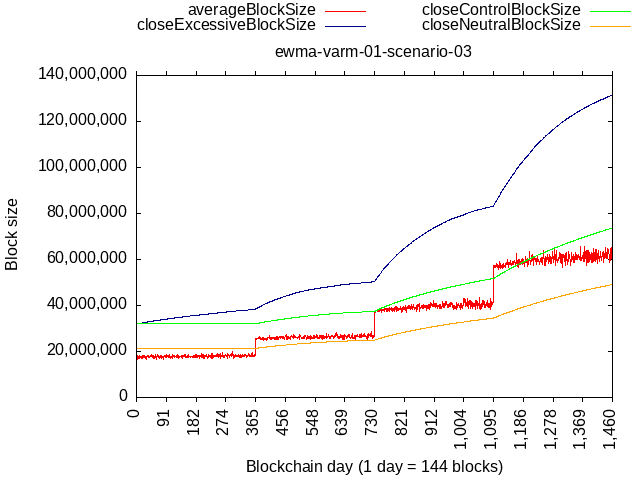
Scenario 03
- Year 1: 10% at 100% fullness, 90% at 16 MB
- Year 2: 10% at 100% fullness, 90% at 24 MB
- Year 3: 10% at 100% fullness, 90% at 36 MB
- Year 4: 10% at 100% fullness, 90% at 54 MB
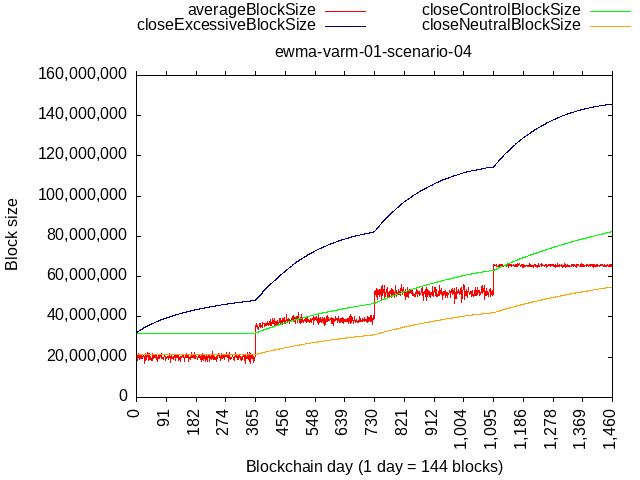
Scenario 04
- Year 1: 50% at 32 MB, 50% at 8 MB
- Year 2: 20% at 64 MB, 80% at 32 MB
- Year 3: 30% at 80 MB, 70% at 40 MB
- Year 4: 10% at 80 MB, 90% at 64 MB
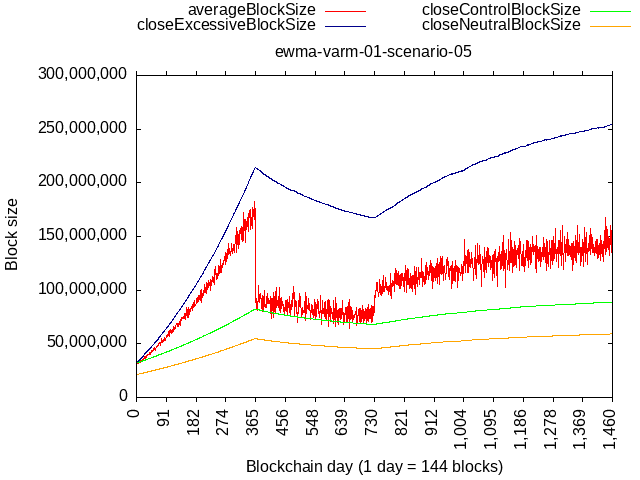
Scenario 05
- Year 1: 80% at 100% fullness, 20% at 24 MB
- Year 2: 33% at 100% fullness, 67% at 32 MB
- Years 3-4: 50% at 100% fullness, 50% at 32 MB
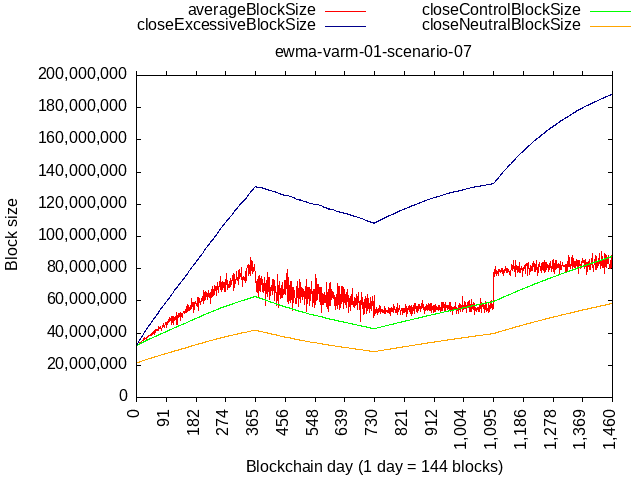
Scenario 07
- Year 1: 50% at 100% fullness, 50% at 32 MB
- Year 2: 50% at 100% fullness, 50% at 8 MB
- Year 3: 10% at 100% fullness, 90% at 48 MB
- Year 4: 10% at 100% fullness, 90% at 72 MB
In general I have seen this topic being discussed now for about 7 years, first talks about something like this started on Reddit.com in 2016 or so, maybe even earlier.
I have also seen you work on tweaks for this and previous, similar algorithm [maybe it was the same and this is the upgraded version] for about 2 years.
I think this code could easily be reaching a production-ready stage right now. Am I wrong here?
It has seen many iterations but the core idea was the same: observe the current block and based on that slightly adjust the limit for the next block, and so on. I believe that the current iteration now does the job we want it to do. Finding the right function and then proving it’s the right function takes the bulk of work and the CHIP process.
The code part is the easy part  Calin should have no problems porting my C implementation, the function is just 30 lines of code.
Calin should have no problems porting my C implementation, the function is just 30 lines of code.
Truly Excellent!
Over the last few days I had an extensive discussion with @jtoomim on Reddit, his main concern is this:
This does not guarantee an increase in the limit in the absence of demand, so it is not acceptable to me. The static floor is what I consider to be the problem with CHIP-2023-01, not the unbounded or slow-bounded ceiling.
BCH needs to scale. This does not do that.
and he proposed a solution:
My suggestion for a hybrid BIP101+demand algorithm would be a bit different:
- The block size limit can never be less than a lower bound, which is defined solely in terms of time (or, alternately and mostly equivalently, block height).
- The lower bound increases exponentially at a rate of 2x every e.g. 4 years (half BIP101’s rate). Using the same constants and formula in BIP101 except the doubling period gives a current value of 55 MB for the lower bound, which seems fairly reasonable (but a bit conservative) to me.
- When blocks are full, the limit can increase past the lower bound in response to demand, but the increase is limited to doubling every 1 year (i.e. 0.0013188% increase per block for a 100% full block).
- If subsequent blocks are empty, the limit can decrease, but not past the lower bound specified in #2.
My justification for this is that while demand is not an indicator of capacity, it is able to slowly drive changes in capacity. If demand is consistently high, investment in software upgrades and higher-budget hardware is likely to also be high, and network capacity growth is likely to exceed the constant-cost-hardware-performance curve.
This is easily achievable with this CHIP, I just need to tweak the max() part to use a calculated absolutely-scheduled y_0 instead of the flat one.
There were some concerns about algorithm being too fast - like what if some nation-state wants to jump on-board and it pushes the algorithm beyond what’s safe considering technological advancement trajectory. For that purpose we could use BIP101 as the upper bound, and together get something like this:
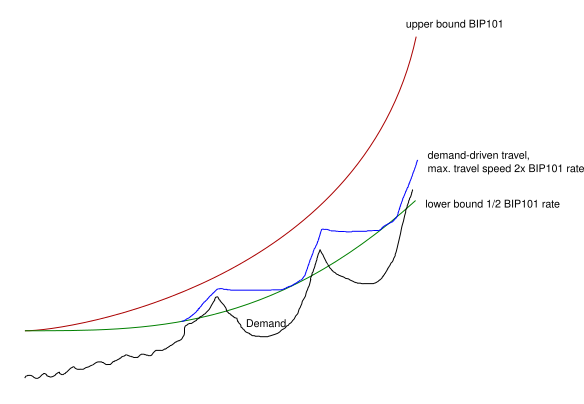
To get the feel for what the upper & lower bounds would produce, here’s a table:
| Year | Lower Bound (Half BIP-0101 Rate) | Upper Bound (BIP-0101 Rate) |
|---|---|---|
| 2016 | NA | 8 MB |
| 2020 | 32 MB | 32 MB |
| 2024 | 64 MB | 128 MB |
| 2028 | 128 MB | 512 MB |
| 2032 | 256 MB | 2,048 MB |
| 2036 | 512 MB | 8,192 MB |
If there’s no demand, our limit would stick to lower bound. If there’s demand, our limit would move towards the upper bound. The scheduled lower bound means recovery from a period of inactivity will be easier with time since at worst it would be starting from a higher base - determined by the lower bound.
Posted on Reddit too, just copying here:
Very impressive work, thank you for your time and energy on this /u/bitcoincashautist!
I think this is already a huge improvement from a fixed limit, and adopting a dynamic limit doesn’t preclude future CHIPs from occasional bumping the minimum cap to 64MB, 128MB, 256MB, etc.
I’m most focused on development of applications and services (primarily Chaingraph, Libauth, and Bitauth IDE) where raising the block size limit imposes serious costs in development time, operating expenses, and product capability. Even if hardware and software improvements technically enable higher limits, raising limits too far in advance of real usage forces entrepreneurs to wastefully redirect investment away from core products and user-facing development. This is my primary concern in evaluating any block size increase, and the proposed algorithm correctly measures and minimizes that potential waste.
As has been mentioned elsewhere in this thread, “potential capacity” (of reasonably-accessible hardware/software) is another metric which should inform block size. While excessive unused capacity imposes costs on entrepreneurs, insufficient unused capacity risks driving usage to alternative networks. (Not as significantly as insufficient total capacity as prior to the BTC/BCH split, but the availability of unused capacity improves reliability and may give organizations greater confidence in successfully launching products/services.)
Potential capacity cannot be measured from on-chain data, and it’s not even possible to definitively forecast: potential capacity must aggregate knowledge about the activity levels of alternative networks (both centralized and decentralized), future development in hardware/software/connectivity, the continued predictiveness of observations like Moore’s Law and Nielsen’s Law, and availability of capital (a global recession may limit widespread access to the newest technology, straining censorship resistance). We could make educated guesses about potential capacity and encode them in a time-based upgrade schedule, but no such schedule can be definitively correct. I expect Bitcoin Cash’s current strategy of manual forecasting, consensus-building, and one-off increases may be “as good as it gets” on this topic (and in the future could be assisted by prediction markets).
Fortunately, capacity usage is a reasonable proxy for potential capacity if the network is organically growing, so with a capacity usage-based algorithm, it’s possible we won’t even need any future one-off increases.
Given the choice, I prefer systems be designed to “default alive” rather than require future effort to keep them online. This algorithm could reasonably get us to universal adoption without further intervention while avoiding excessive waste in provisioning unused capacity. I’ll have to review the constants more deeply once it’s been implemented in some nodes and I’ve had the chance to implement it in my own software, but I’ll say I’m excited about this CHIP and look forward to seeing development continue!
Guys, the algorithm could work either way (the old pre-jtoomin version and the new jtoomin++ version) while not causing any damage/disaster/problems for years, so right now my only concern is getting this done for 2024 upgrade.
We cannot really afford to wait. Waiting any longer or inducing another years-long bikeshedding debates is really dangerous to the continuous survival of this project. In the 2-3-5 years future we could end up with another “what is the proper blocksize” debate and face another Blockstream takeover situation, so I think everybody here would want to avoid this at any cost.
As I said 10 times already, the main problem to solve here is social, not technological. It’s about etching the need for regular maximum automatic blocksize increase into the minds of users and the populace so we do not need to deal with anti-cash divide & conquer propaganda in next years. Because people, in their mass, follow and not think. So making a social & psychological strong pattern is the most logical course of action.
An algorithm, even one that is just very good and not perfect in every way, will do. We can start with “very good” and achieve “perfect” in next years. Nobody is stopping anybody from making a CHIP and improving this algorithm in 2025 or 2026.
I think it is crucial that everybody here understands this.
Reddit user d05CE realized we can break up the problem into 3 conceptual problems:
The key breakthrough that helps address all concerns is the concept of min, max, and demand.
min = line in the sand baseline growth rate = bip101 using a conservative growth rate
demand algo = moderation of growth speed above baseline growth to allow for software dev, smart contract acclimation to network changes, network monitoring, miner hardware upgrades and possibly improved decentralization. We can also monitor what happens to fees as blocks reach 75% full for example instead of hitting a hard limit. It basically is a conservative way to move development forward under heavy periods of growth and gives time to work through issues should they arise.
max = hardware / decentralization risk comfort threshold = bip101 using neutral growth rate
I hope to demonstrate why there’s no need for neither fixed-schedule minimum nor fixed-schedule maximum.
Upper Bound
Let’s address the maximum first, because I’ve observed it’s a common concern about algorithm being too fast (and the argument of it meaning there’s effectively no limit).
Could spammy miners be able to quickly work it into an unsustainable size and capture the network (like on BSV)?
Or, what if there’s just so much natural demand that it’s actually proper fee-paying transactions that are causing the TX load and driving the algorithm, causing a tragedy of the commons?
Could tech development keep up even at extreme demand?
It’s true that the algorithm is open-ended, but it is rate-limited by the chosen constant gamma. The constant determines the maximum speed, and after talking with @jtoomim I realized the 4x/year rate-limit was too generous - and he proposed 2x/year, and I tested it and it looks good, see below.
The original BIP-101 curve is deemed as a good estimate of tech. capabilities, what would it take to catch up with original BIP-101 curve?
With updated constants, consider an extreme scenario of 90% blocks being 90% full, while the remaining 10% hash-rate having a self-limit of 21 MB:
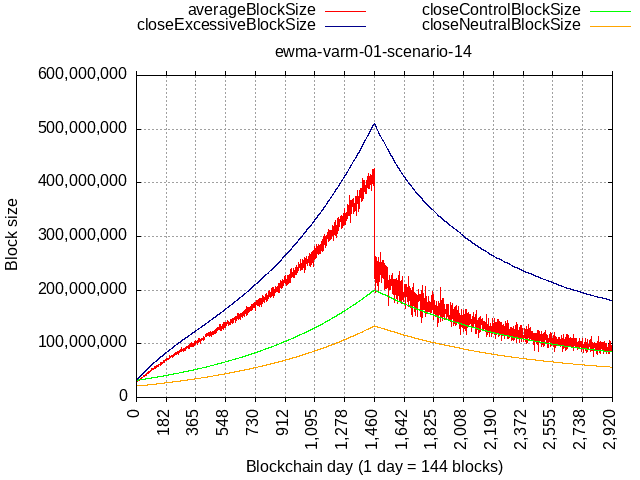
The relative rate here is higher than BIP-101, but because we’d be starting from 32 MB base, it would be able to catch up with original BIP-101 schedule (512 MB in '28) only after 4 years of such extreme network load.
Taken to the theoretical extreme not really achievable in practice – that of 100% blocks full 100% of the time, it could cross over BIP-101 sooner, but it would still take about 1.25 years (256 MB Q1 of '25).
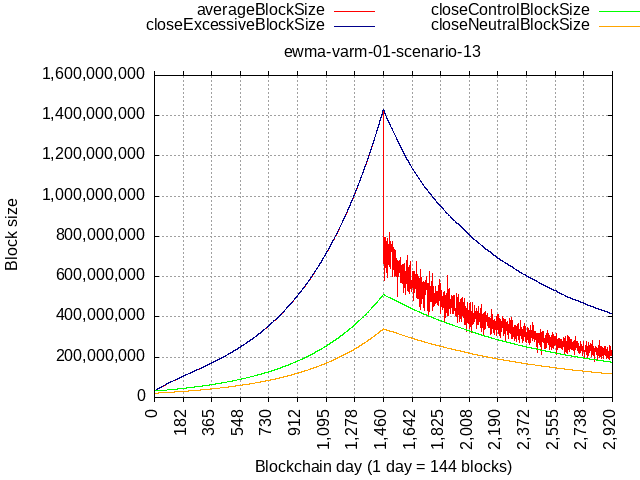
Also note that such max. load scenario would have to start in '24 immediately with activation. Delayed start of TX load (or insufficient load) means the BIP-101 curve will be making make more distance.
Delayed or insufficient TX load means that any period of lower activity extends the runway, extends the time it would take to catch up with absolutely-scheduled BIP-101 curve.
What about a big pool trying to game and abuse the algorithm by stuffing blocks with their own transactions?
Even if the adversary pool had 50% hash-rate and stuffed their blocks to 100% full, the remaining 50% self-limiting to flat 21 MB would stabilize the limit at about 120 MB (which is technologically safe even now), and it would take 4 years to get there.
If the remaining 50% then lifted their limit to 42 MB, they’d be allowing the spammer to grow it to about 240 MB and it would take 4 more years.
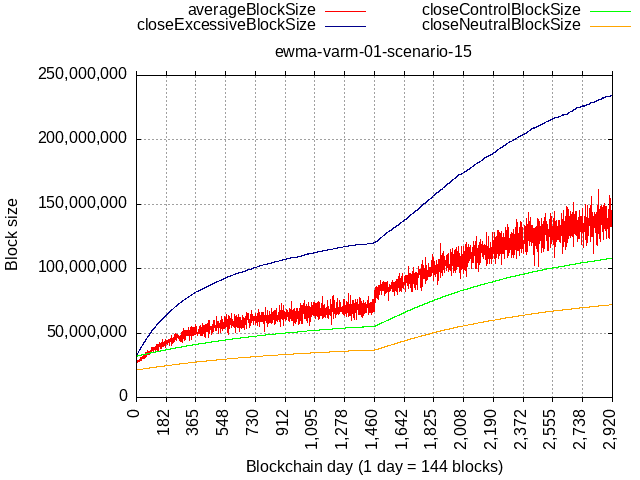
If the spammy hash-rate had “only” 33% hashrate, it would result in almost 2x lower limit at the equilibrium.
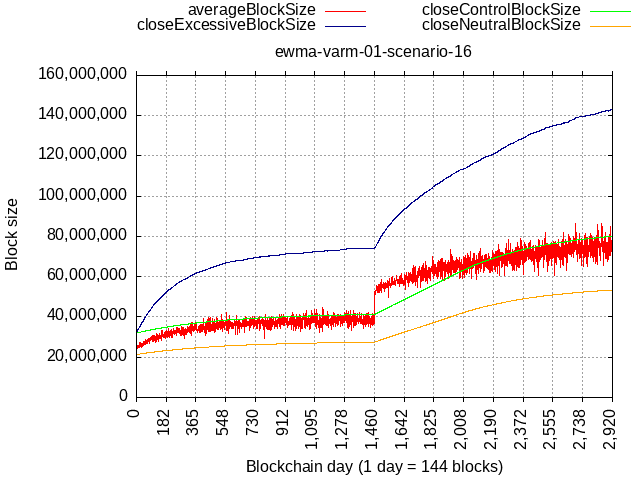
Satisfying Demand
Would it be too slow to satisfy demand even if tech limits allowed it? At beginning surely not, since 32 MB is the algo’s fixed floor, and we’re only using few 100 kBs so plenty of burst capacity. What about later, once adoption picks up and miners start allowing blocks above 21 MB (adjusting their self-limit)?
Consider this scenario:
- Y1 - Y2Q3: 10% blocks at max, 90% at 21 MB
- Y2Q4: burst to 50% blocks at max, 90% at 21 MB
- Y3 - Y3Q3: again 10% blocks at max. (but max is now bigger) + new baseline of 32 MB (90% blocks),
- Y4Q4: burst to 50% blocks at max, 90% at 32 MB
- onward: again 10% blocks at max. (but max is now bigger) + 32 MB (90% blocks),
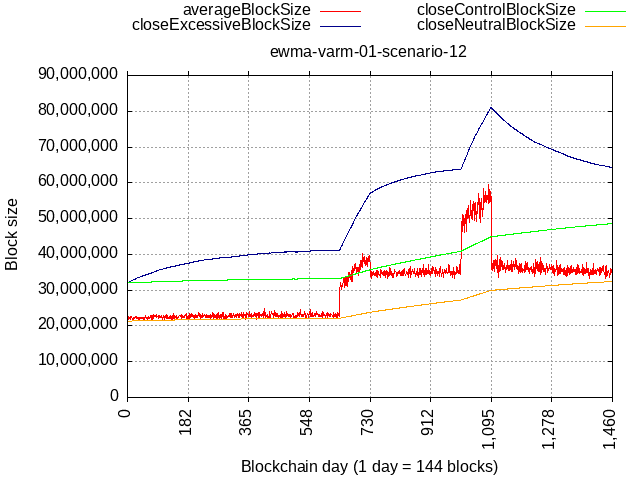
How about actual data from Ethereum network?
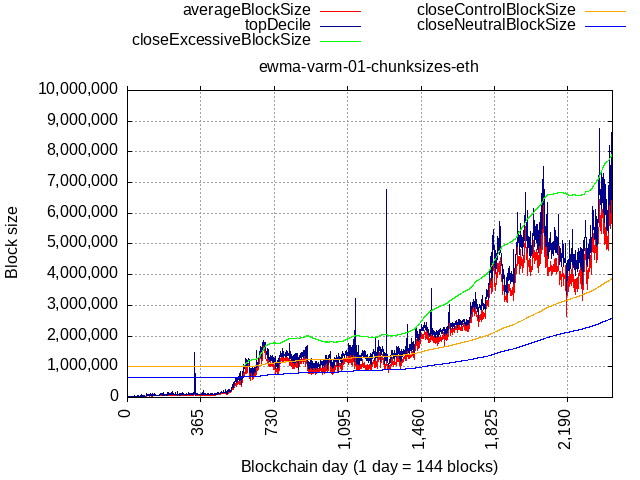
There could be a few pain points in case of big bursts of activity, but it would be a temporary pain quickly to be relieved.
Lower Bound
As it is being proposed, the lower bound is flat 32 MB, to match the current flat limit, so any extra room by the algorithm can be thought of as a bonus space on top of the 32 MB lower bound, which would be maintained even if no activity.
The above plots also show us that if activity keeps making higher lows, then a natural, dynamic, lower bound will be formed. The recent dip in Ethereum’s network activity was still above the neutral size curve and kept moving the baseline higher even though the limit didn’t move due to buffer zone decaying. It would have never came back down to the flat lower bound (set to 1 MB for that plot).
Some extreme scenario, like a fork taking away 90% of pre-fork TX load would cause the limit to go back to the flat lower bound, but not below.
Consider an example of actual BTC+BCH data but if flat lower bound were to be 1 MB. After the fork, limit would go back down almost to 1 MB, which would’ve been too much below '23 tech capabilities and would warrant a coordinated “manual” adjustment of the flat lower bound.
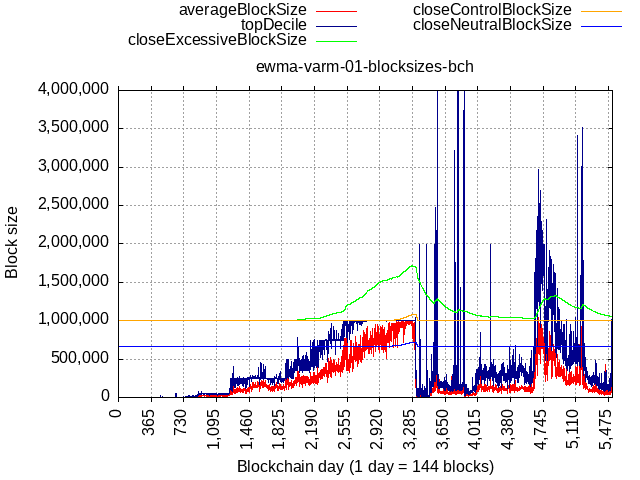
I agree with comments here that miners are generally not innovators. They are risk averse. Miners follow mining pools and mining pools follow each other. This behavior creates a deadlock: everyone is waiting for someone else to move, so no one does. I am not persuaded by arguments that the free market will solve this coordination problem.
IMHO, this conclusion is supported by the data. In my research I discovered that Monero mining pools were leaving fee revenue “on the table” until recently. They did not update their block templates with new transactions except when a new block was found. This delayed transaction confirmations by about 60 seconds on average. Most Monero mining pools changed their block update configurations after I released my analysis:
https://www.reddit.com/r/Monero/comments/10gapp9/centralized_mining_pools_are_delaying_monero/
I support a coordination mechanism to adjust BCH’s block size.
I may have missed it, but I did not see anyone try to analyze this CHIP’s effect on miners’ fee revenue. In the long term, miners’ fee revenue protects the whole system.
The bitcoin white paper says:
Once a predetermined number of coins have entered circulation, the incentive can transition entirely to transaction fees and be completely inflation free.
The incentive may help encourage nodes to stay honest. If a greedy attacker is able to assemble more CPU power than all the honest nodes, he would have to choose between using it to defraud people by stealing back his payments, or using it to generate new coins. He ought to find it more profitable to play by the rules, such rules that favour him with more new coins than everyone else combined, than to undermine the system and the validity of his own wealth.
This obviously isn’t the whole story. A “greedy attacker” can execute a 51% attack to acquire something of value that is not bitcoin. In that case, he does not care about “undermin[ing] the system and the validity of his own wealth” since his wealth is no longer in bitcoin. An attacker does not have to be greedy. A 51% attack can occur as sabotage. Governments or anyone who is against bitcoin could have a reason to execute a sabotaging attack.
IMHO, analysis of this CHIP is incomplete without at least some exploration of possible future fee revenue scenarios. AFAIK, all future transactions paying minrelayfee (currently 1 sat/byte) is an unspoken assumption. Then once the block reward subsidy become negligible the security budget will amount to bytes per block * minrelayfee * purchasing power of one BCH satoshi. Is that going to give BCH enough security?
Huberman, Leshno, & Moallemi (2021). “Monopoly without a Monopolist: An Economic Analysis of the Bitcoin Payment System.” rigorously analyzes how miner fee revenue reacts to user demand for block space and block size limits.
Budish (2022). “The Economic Limits of Bitcoin and Anonymous, Decentralized Trust on the Blockchain.” evaluates several attack scenarios against bitcoin’s proof-of-work security model.
While I have been extremely supportive of @bitcoincashautist’s work on developing a self-adjusting block size limit, I have been very skeptical of his approach so far because I didn’t think that it addressed certain issues with gameability and I didn’t think he had a good answer for the question “why should demand drive what is essentially an issue of supply?”
This proposal and his explanations address my issues. With this proposal, block sizes cannot be gamed above or below established guardrails. Demand is used to provide a damping factor that prevents sudden shocks to the limit, so that if the limit is running near the lower bounds tolerated by the algo, it cannot suddenly adjust to the upper bounds. This allows network operators time to recognize and adjust to changing demand and further disincentivises gaming the system.
As others pointed out, I think it’s a real breakthrough to think of the limit in terms of a minimum, maximum, and a demand-based “rate of change” damping factor. Framing the solution in this manner also improves future enhancements, because we have devolved the problem into three distinct issues, each independently addressable. If the damping factor is too fast or slow (ie the limit oscillates excessively) we can tighten it without having to modify the guardrails. If there is a discontinuous jump in network capability due to a hardware or software breakthrough, we can relax the guardrails without changing the damping factor.
ACK
While I agree completely with your argument about 51% attacks, requiring this CHIP to demonstrate future fee scenarios is out of scope and the question “will there be enough security” is unanswerable and a red herring. I disagree that it’s important to consider in the context of this proposal. Here’s my poorly organized response:
As the not-BTC, BCH should never consider itself in the business of developing a “fee market.” BTC is competing on fixed supply and high fees; we are competing on fixed (always low) fees and high supply.
If the always-low fees don’t generate enough utilization, then one day, BCH will fail. Conversely, on BTC, if the always-low supply doesn’t generate enough fee pressure, then one day, BTC will fail. As you point out, both depend on future demand (which is unknowable) and future purchasing power (aka price in the fiat world) which is also unknowable.
Since BCH is inherently “low fee/high utilization” the only way for BCH to pay for security in the long term while remaining true to its goals is to have enough transactions paying the minfee. So the only negative this proposal could possibly introduce is to excessively limit block size one day in a distant future where millions of people want to make so many BCH transactions that we hit the maximum allowed, which constrains revenue assuming the minfee. Which is what we call a great problem to have because it implies BCH has really succeeded! But then, we will be generating a fee market – which is not in line with our goals, but which should be able to pay for continued security.
So in a nutshell: regarding future revenue generation, this proposal is categorically better than what we have now (fixed limit), and in no way can it be worse (cannot drop below what we have now). Since perfect is the enemy of good, and since the algo can be improved going forward, I don’t think this is an issue at all.
As I said 10 times already, the main problem to solve here is social, not technological . It’s about etching the need for regular maximum automatic blocksize increase into the minds of users and the populace so we do not need to deal with anti-cash divide & conquer propaganda in next years. Because people, in their mass, follow and not think. So making a social & psychological strong pattern is the most logical course of action.
An algorithm, even one that is just very good and not perfect in every way, will do. We can start with “very good” and achieve “perfect” in next years. Nobody is stopping anybody from making a CHIP and improving this algorithm in 2025 or 2026.
I agree 100% with Shadow on this and urge people to prioritize this upgrade for 2024 if at all possible for all the reasons that he gave.
It shouldn’t have an effect, because unlike Monero’s – the algo doesn’t require fee pressure to build up in order to start moving, there’s no miner penalty so users don’t have to “buy” an increase. The limit would float 2-3x above average block size usage even if all TXs were paying only the min. relay fee (whatever the value of it), or even 0-fee (miner’s own TXs). All mined bytes are treated equal from PoV of the algo, and economic decisions are left to users and miners to negotiate.
The algo is not supposed to mess with the fees or put artificial pressure on them. If miners adjust their flat self-limits in discrete steps, and it’s supported by TX volume (someone has to make all those TXs), then the algo would work to provide space for the next bump of their self-limits. Some may go for 100%, some may stay at flat, up to them, the natural limit to their self-limit is their orphan rates - at which point either propagation tech improves or users have to start paying more in fees if the TX load keeps increasing while tech does not - but in that case fee pressure would not be because of the algo, it would be due to miner’s self-limits. Peter Rizun wrote on it ages ago: https://www.bitcoinunlimited.info/resources/feemarket.pdf
The algo’s limit is open-ended and limit supported by whatever “baseload” TX volume our network can attract. The algo would just be continuously making room for it as it organically comes, agnostic of fees.
Yes, some analysis of behavior under a simulated mempool load would be interesting, but I feel here it would be a nice to have, and absence of it should not be blocking us from activating the CHIP.
This is orthogonal to the algo. Algo is agnostic of relay fee policy. If everyone agreed tomorrow to lower it to 0.1sat/byte then nothing would change from PoV of the algo - all it sees is block sizes, doesn’t care why they have the size they have - that’s up to network participants to negotiate - miners to allow the volume by lifting their self-limits and users to make the TX volume to produce the bytes to be mined and counted by the algo. The algo will simply provide negotiating space as use of our block space ramps up.
Security budget will come from a high volume of fees, and algo will make room for it when TX volume starts coming. This could mean 100 MB blocks of 0.1sat/byte at $100k price point, so $10k/block or $1.44M/day 
To say that EBAA is orthogonal to miner revenue or out of its scope is to argue that the supply curve of a service has no effect on price or revenue. In other words, the argument is incorrect.
regarding future revenue generation, this proposal is categorically better than what we have now (fixed limit), and in no way can it be worse (cannot drop below what we have now)
There can be greater total miner revenue by restricting the supply of block space. If you want a rigorous argument, read Huberman, Leshno, & Moallemi (2021). If you want empirical support, look at BTC miner fee revenue. You may think it is undesirable to restrict block space, let’s be sure to have the discussion on a solid economic foundation.
This CHIP seems to aim to avoid any fee market. That’s fine, but that decision has consequences. It is OK to say “we are kicking this can down the road”. After all, arguably EBAA is a can that has been kicked down the BCH road since 2017, yet BCH has not experienced any severe problems from not addressing the can until now. However, there is going to have to be a reckoning on fee revenue at some point.
No, because it’s not the EB limit which determines the supply curve, but aggregate of miner’s individual self-limits weighted by their relative hash-rate.
There can be greater total miner revenue by restricting the supply of block space.
Miners are free to play the supply-restriction game, but they don’t play it in vacuum.
BTC loses users with every “fee event”, and LTC has been the biggest winner.
Users simply nope-out, and go to other networks.
With artificial limit on total volume, who will pay for security between bull runs?
To have the nodes set a limit with the objective to exert an artificial fee pressure is to fall into the central planner’s trap.
Once upon a time, when Bitcoin (BTC) still had freedom of thought, there was an inspiring post about our long-term future: https://www.reddit.com/r/Bitcoin/comments/3ame17/a_payment_network_for_planet_earth_visualizing/
It is Bitcoin Cash ethos that aim to avoid artificial fee market, and the CHIP preserves that spirit.
We have been kicking the can (2 kicks so far, to 8, and then to 32), yes, and we’re committed to continuing kicking the can, and the EBAA will be a can auto-kicker so we don’t have to keep spending “meta” energy to execute further kicks.
Our success scenario looks like this: 1 GB blocks, $1M price, and still $0.01 fee / TX.
That would be $50k / block on top of whatever block reward subsidy we’d have when we reach the milestone.
Avoiding a fee market is a core goal of BCH, not this CHIP. “Fee pressure” should only occur when demand exceeds actual realizable capacity and not some artificial scarcity imposed by miners or devs. Ideally, with hardware and software improvements, demand will never exceed realizable capacity and there will never be a fee market.
In that regard, this CHIP is consistent with these goals and categorically superior to what we have now because it prevents either miners or devs from blocking possible capacity increases by refusing to change the artificial limits.
Just to nitpick / amplify this, our success scenario looks like this: 1 GB blocks, $1M price, and still $0.01 fee / TX.
Price should be irrelevant. Price only figures into this when you factor in the subsidy. BCH can pay $50K/block for its security even if price is $100 if there are 1GB blocks paying $0.01 per txn. The subsidy is just icing on the cake at that point.
Well I agree it should. But it won’t.
Because the herd/the populace perceives something as desirable proportionally to its price and reverse: when something becomes perceived as more desirable, its price also rises. So when BCH begins being perceived as amazing by most people on the planet, these will be the consequences.
It’s just evolution, human instincts, we cannot skip it. So unfortunately we have to live with this.
Personally I am fine with BCH being valued at $1M a coin. It won’t be easy, but I am prepared to bear this burden and inconvenience.
What is required in order to confirm this feature for the next major upgrade cycle? I agree with Shadow, this is something that can be bikeshedded ad infinitum. The current proposal satisfies all significant concerns and is a big step up both technically and from a marketing perspective. Let’s push this off dead center and get it in the works.