Reddit user d05CE realized we can break up the problem into 3 conceptual problems:
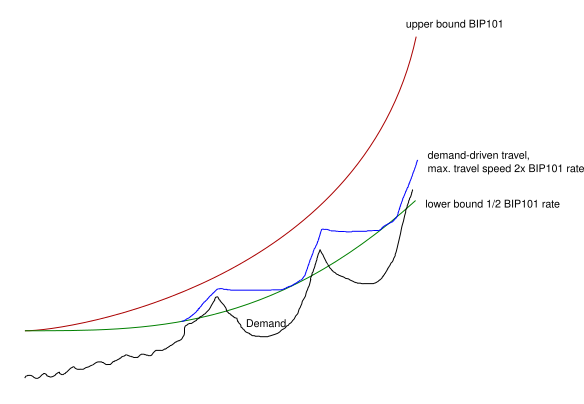
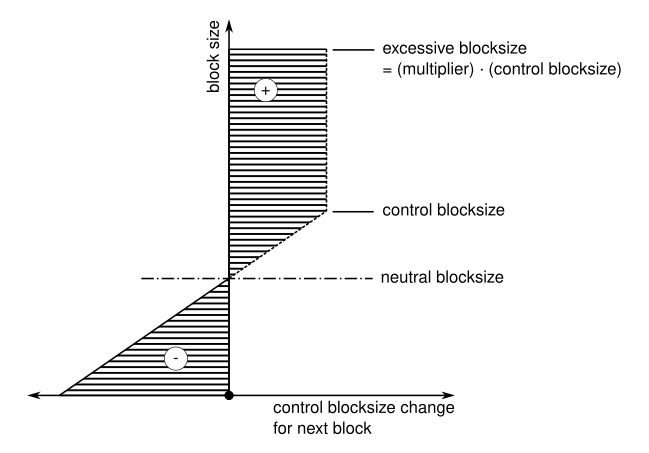
The key breakthrough that helps address all concerns is the concept of min, max, and demand.
min = line in the sand baseline growth rate = bip101 using a conservative growth rate
demand algo = moderation of growth speed above baseline growth to allow for software dev, smart contract acclimation to network changes, network monitoring, miner hardware upgrades and possibly improved decentralization. We can also monitor what happens to fees as blocks reach 75% full for example instead of hitting a hard limit. It basically is a conservative way to move development forward under heavy periods of growth and gives time to work through issues should they arise.
max = hardware / decentralization risk comfort threshold = bip101 using neutral growth rate
I hope to demonstrate why there’s no need for neither fixed-schedule minimum nor fixed-schedule maximum.
Upper Bound
Let’s address the maximum first, because I’ve observed it’s a common concern about algorithm being too fast (and the argument of it meaning there’s effectively no limit).
Could spammy miners be able to quickly work it into an unsustainable size and capture the network (like on BSV)?
Or, what if there’s just so much natural demand that it’s actually proper fee-paying transactions that are causing the TX load and driving the algorithm, causing a tragedy of the commons?
Could tech development keep up even at extreme demand?
It’s true that the algorithm is open-ended, but it is rate-limited by the chosen constant gamma. The constant determines the maximum speed, and after talking with @jtoomim I realized the 4x/year rate-limit was too generous - and he proposed 2x/year, and I tested it and it looks good, see below.
The original BIP-101 curve is deemed as a good estimate of tech. capabilities, what would it take to catch up with original BIP-101 curve?
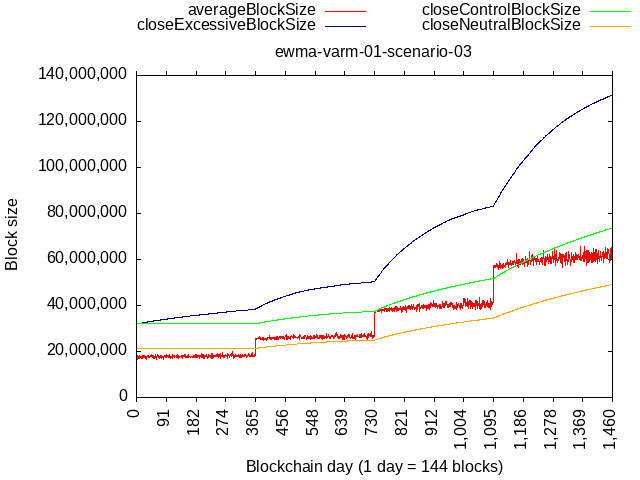
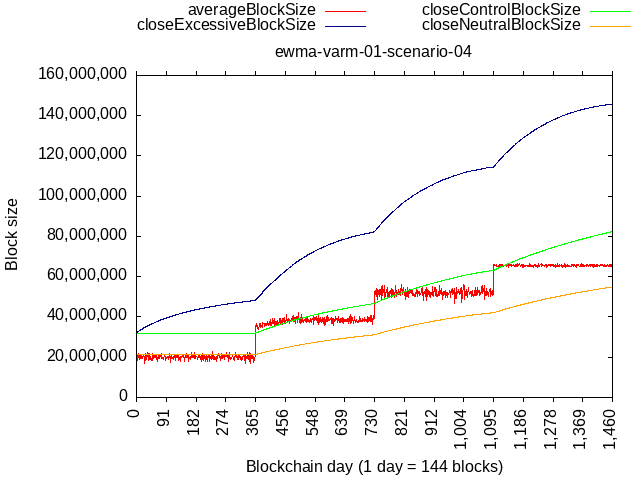
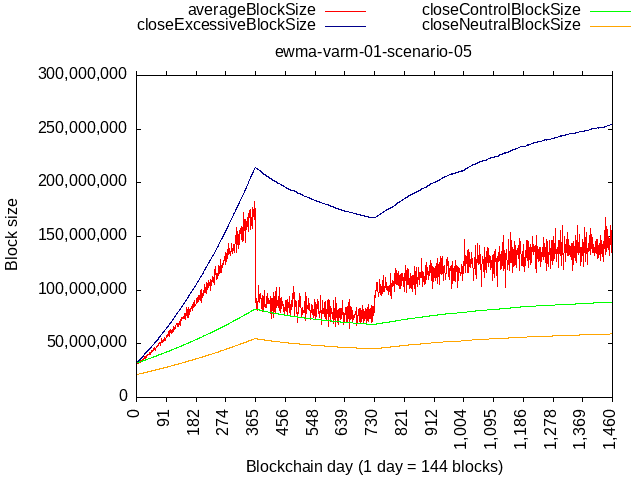
With updated constants, consider an extreme scenario of 90% blocks being 90% full, while the remaining 10% hash-rate having a self-limit of 21 MB:
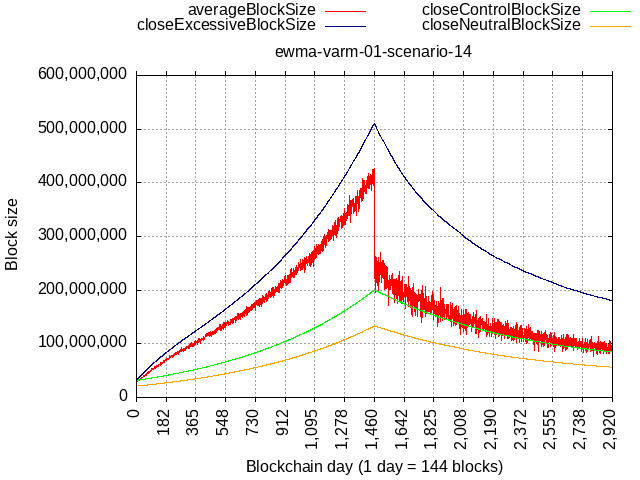
The relative rate here is higher than BIP-101, but because we’d be starting from 32 MB base, it would be able to catch up with original BIP-101 schedule (512 MB in '28) only after 4 years of such extreme network load.
Taken to the theoretical extreme not really achievable in practice – that of 100% blocks full 100% of the time, it could cross over BIP-101 sooner, but it would still take about 1.25 years (256 MB Q1 of '25).
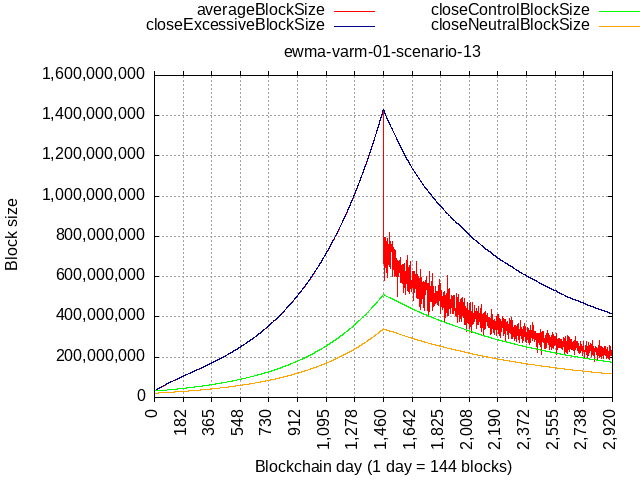
Also note that such max. load scenario would have to start in '24 immediately with activation. Delayed start of TX load (or insufficient load) means the BIP-101 curve will be making make more distance.
Delayed or insufficient TX load means that any period of lower activity extends the runway, extends the time it would take to catch up with absolutely-scheduled BIP-101 curve.
What about a big pool trying to game and abuse the algorithm by stuffing blocks with their own transactions?
Even if the adversary pool had 50% hash-rate and stuffed their blocks to 100% full, the remaining 50% self-limiting to flat 21 MB would stabilize the limit at about 120 MB (which is technologically safe even now), and it would take 4 years to get there.
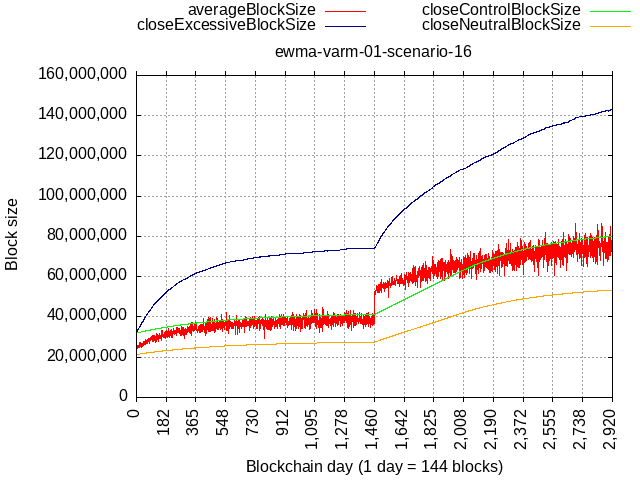
If the remaining 50% then lifted their limit to 42 MB, they’d be allowing the spammer to grow it to about 240 MB and it would take 4 more years.
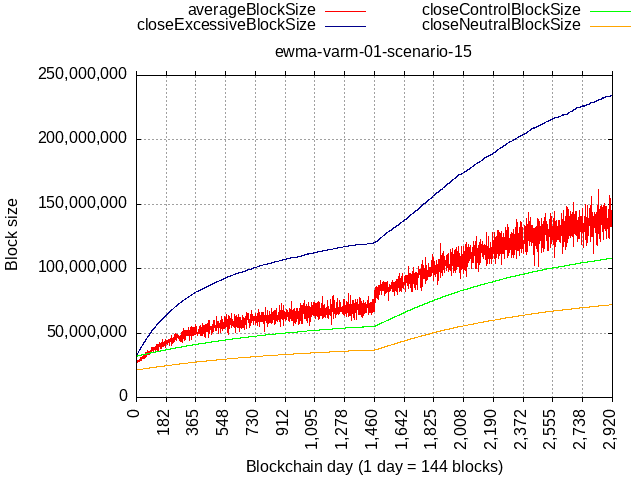
If the spammy hash-rate had “only” 33% hashrate, it would result in almost 2x lower limit at the equilibrium.
Satisfying Demand
Would it be too slow to satisfy demand even if tech limits allowed it? At beginning surely not, since 32 MB is the algo’s fixed floor, and we’re only using few 100 kBs so plenty of burst capacity. What about later, once adoption picks up and miners start allowing blocks above 21 MB (adjusting their self-limit)?
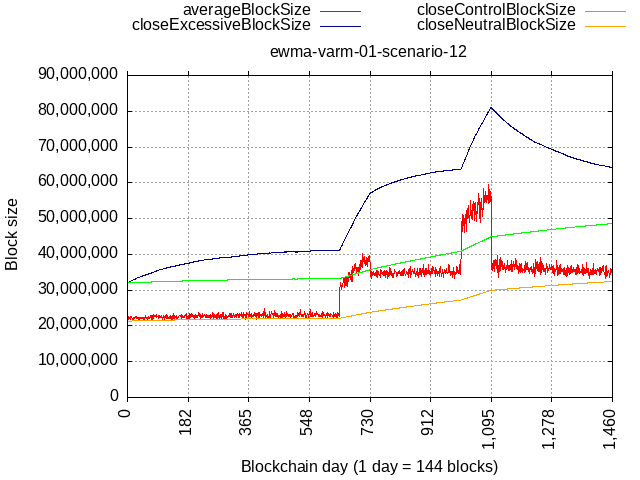
Consider this scenario:
- Y1 - Y2Q3: 10% blocks at max, 90% at 21 MB
- Y2Q4: burst to 50% blocks at max, 90% at 21 MB
- Y3 - Y3Q3: again 10% blocks at max. (but max is now bigger) + new baseline of 32 MB (90% blocks),
- Y4Q4: burst to 50% blocks at max, 90% at 32 MB
- onward: again 10% blocks at max. (but max is now bigger) + 32 MB (90% blocks),
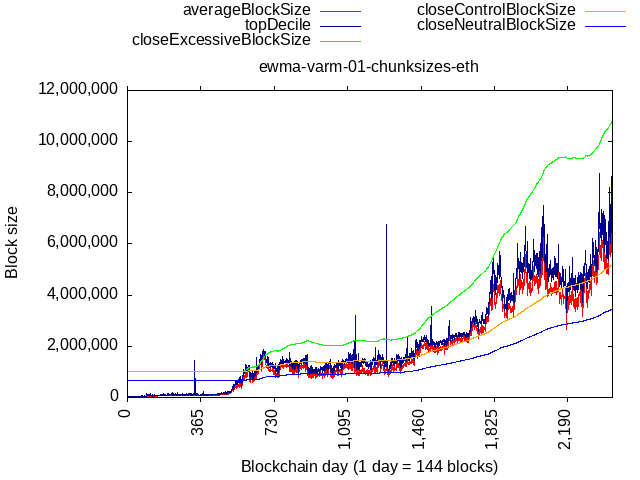
How about actual data from Ethereum network?
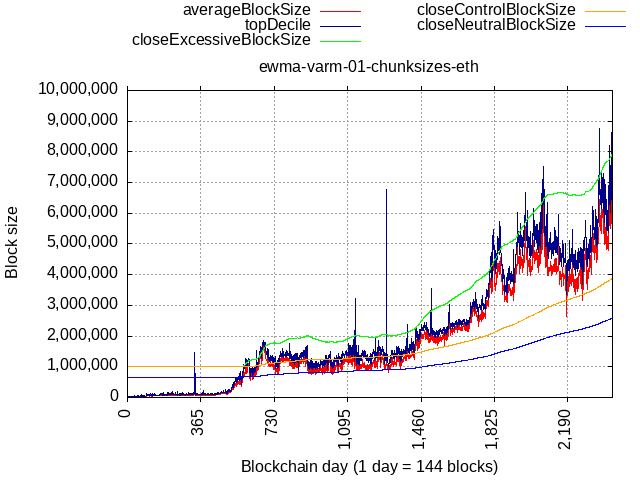
There could be a few pain points in case of big bursts of activity, but it would be a temporary pain quickly to be relieved.
Lower Bound
As it is being proposed, the lower bound is flat 32 MB, to match the current flat limit, so any extra room by the algorithm can be thought of as a bonus space on top of the 32 MB lower bound, which would be maintained even if no activity.
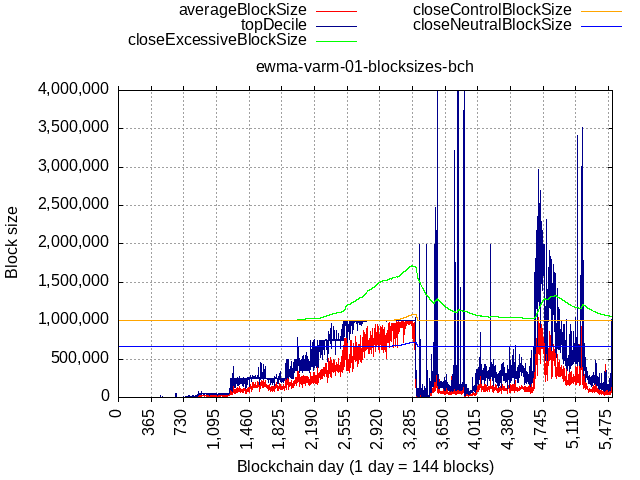
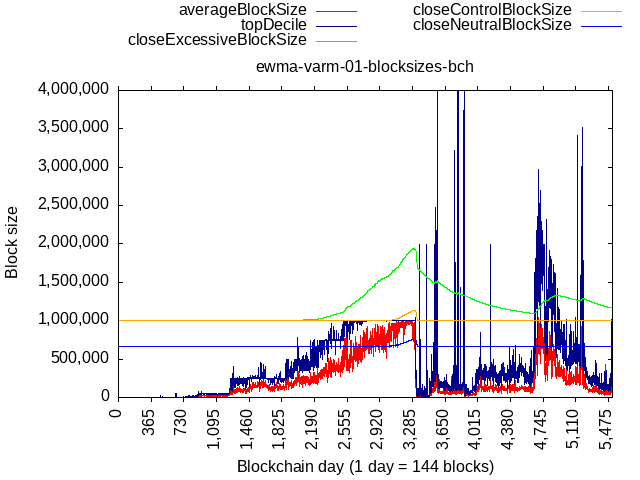
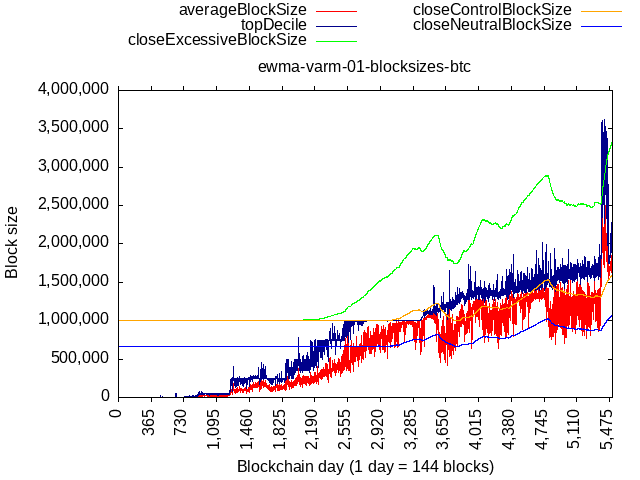
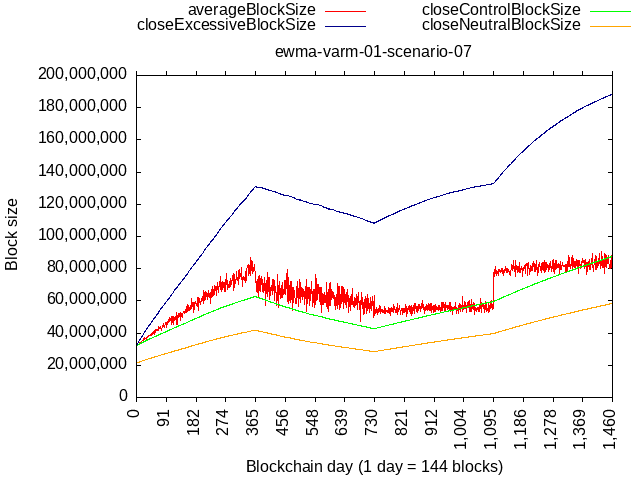
The above plots also show us that if activity keeps making higher lows, then a natural, dynamic, lower bound will be formed. The recent dip in Ethereum’s network activity was still above the neutral size curve and kept moving the baseline higher even though the limit didn’t move due to buffer zone decaying. It would have never came back down to the flat lower bound (set to 1 MB for that plot).
Some extreme scenario, like a fork taking away 90% of pre-fork TX load would cause the limit to go back to the flat lower bound, but not below.
Consider an example of actual BTC+BCH data but if flat lower bound were to be 1 MB. After the fork, limit would go back down almost to 1 MB, which would’ve been too much below '23 tech capabilities and would warrant a coordinated “manual” adjustment of the flat lower bound.

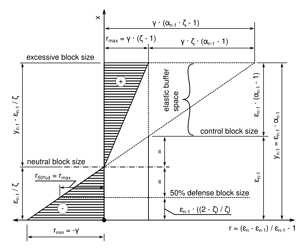
 Calin should have no problems porting my
Calin should have no problems porting my