Empirical analysis of the ASERT's performance

Technical
#1

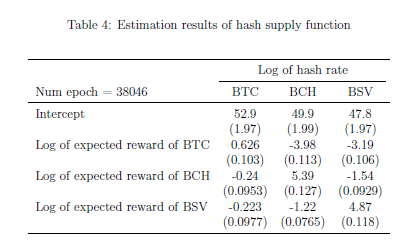
We recently wrote a research paper that empirically investigates the miner’s hash supply response to the difficulty in the SHA-256 currencies using econometrics techniques. In this paper, we evaluated the performance of the DAAs including ASERT, and found that ASERT clearly outperforms CW-144 and BTC’s original DAA.

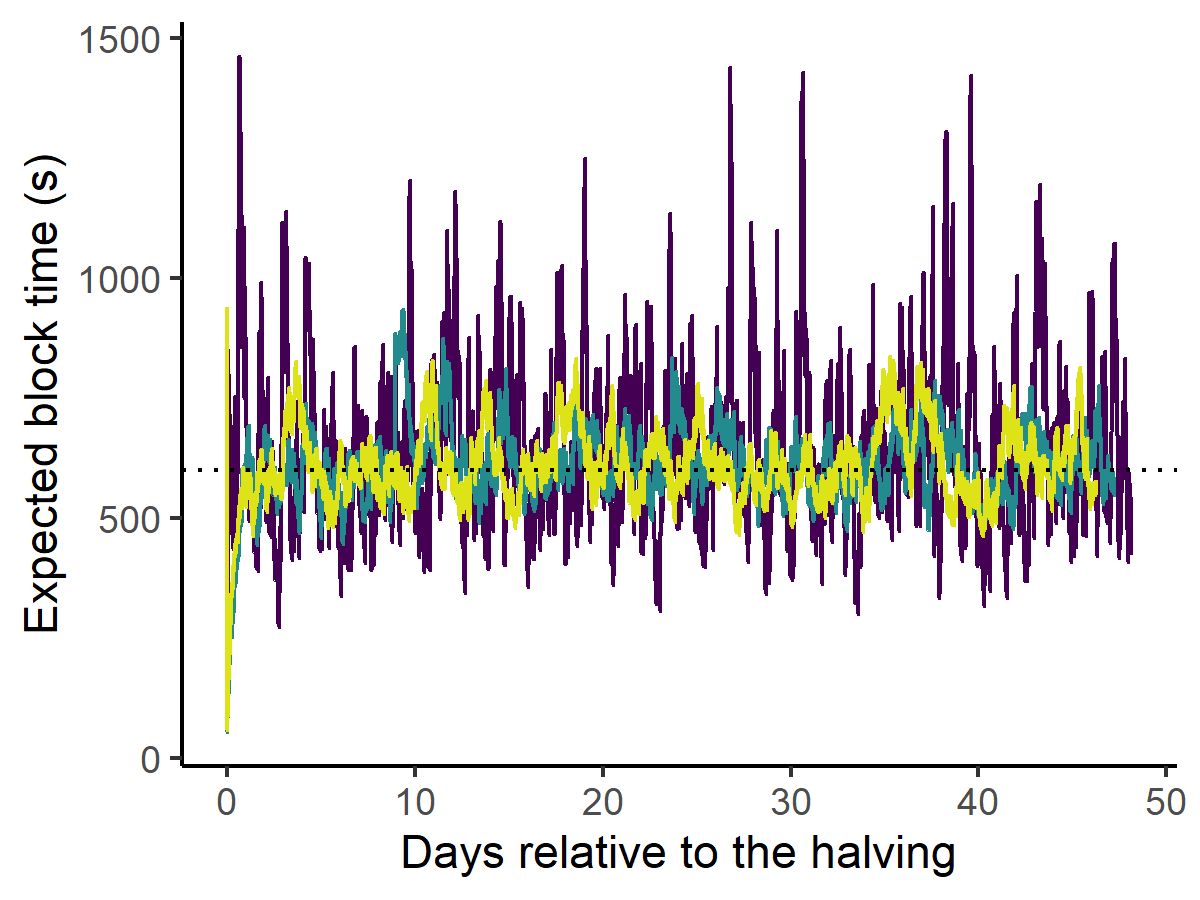
Attached are the key counterfactual simulations results. This is a simulated series of block times starting from the timing of BTC’s third halving. The simulation is based on the estimated miners’ response function to the difficulty, which is inferred from data using econometric techniques. The purple line is the simulated block time when BTC uses the original DAA, BCH uses CW-144, and BSV uses CW-144, the green line is when BCH upgrades to ASERT, and the yellow line is when BTC, BCH, and BSV all upgrade to ASERT. The paper includes other interesting results as well.

I am not sure whether it is okay to post an advertisement for my own papers, but hopefully sharing this helps you to better understand the performance of ASERT.

btc_halving_original_asert_cw144_target_bch_block_time
btc_halving_original_asert_cw144_target_bch_block_time1200×900 21.8 KB

Security-Cost Efficiency of Competing Proof-of-Work Cryptocurrencies

Proof-of-Work cryptocurrencies consume vast energy to rule out potential attacks. Therefore, evaluating and improving the security-cost efficiency, the cost of attacking the system per unit of operating cost, is important. In this paper, we demonstrate that the stability of miners’ supply of work over time is essential for the security-cost efficiency, and it is determined by the Difficulty Adjustment Algorithm (DAA) of the currency and the reward elasticity of the miner’s supply of work. To this end, we develop a model of the multicurrency mining market and estimate the own- and cross-elasticity of the hash supply to the reward by exploiting the reward shock event, called halving. We use the estimated model to simulate the mining market and evaluate the security-cost efficiency. We find that Bitcoin is stable because of the inelastic miners, regardless of the DAA, whereas other smaller coins face highly elastic miners and can be stable only with efficient DAAs. Upgrading all relevant currencies’ DAAs to the state-of-art one substantially improves the security-cost efficiency and saves the energy-consumption rate by 0.21 GW or 3.2% while maintaining the security level.

8 Likes
Lets talk about block time
Asymmetric Moving Maxblocksize Based On Median
Asymmetric Moving Maxblocksize Based On Median
#2

Hey welcome, and thanks for sharing, great to see some fresh research!

#3

Interesting paper. I had two questions I hope you can help me understand. You state:

We find that Bitcoin is stable because of the inelastic miners

  1. I tried to find the evidence for that and couldn’t find exactly that. I found that the paper says the BTC hashrate was inelastic during BCH halving rather than the miners being inelastic. Did I misunderstand? If so, could you explain what it means for miners to be inelastic?
  2. I wasn’t able to quickly understand the measure of inelasticity. If you have time, could you make an introduction to that aspect for someone who isn’t already familiar with all the metrics used?
1 Like
#4

Consider BTC. Let e be the exchange rate (USD/BTC), p is the prize (BTC/block generation), and w is the probability of generating a block per hash (block generation/hash). Then, the expected reward for a miner per hash is r = e * p * w.

The hash rate of BTC is a function of the expected reward per hash. So, it can be written as h(r) = h(e * p * w). We define the elasticity of hash supply to the expected reward as the percent change in h to a 1% change in r. The hash rate is not the hash supply of individual miners but is their sum. Thus, it captures the average characteristics of miners that BTC faces. I hope that this answers q2. The answer to q1 is that “miners to be inelastic” means that the average hash rate of BTC h(r) estimated from the data has the shape such that change in r does not change h at all.

So, how to estimate h(r)? To do so, we focus on the fact that the block arrival rate is approximately a Poisson process whose arrival rate is w * h(r), that is, the winning rate times the hash rate. Therefore, we can write a likelihood of the observed block arrival times as a function of the underlying parameter, which is h(r). Then, we can estimate parameters that maximize the likelihood.

This is the basic idea. But there are a few remaining issues because we consider a multi-currency environment where miners can switch machines across any SHA-256 currency. We properly handled it in the paper.

The estimated elasticity of hash supply to the expected reward is found in Table 4 (attached). It says that the hash rate of BTC drops by 0.62% if the expected reward of BTC drops by 1%, whereas the hash rate of BCH drops by 5.29% if the expected reward of BCH drops by 1% and BSV by 4.87% if the expected reward of BSV drops by 1%. These are called “own” elasticity because it refers to the change in the hash rate of a currency to the change in the expected reward of the currency.

We can also consider the “cross” elasticity, like the % change in the hash rate of BCH to a 1% change of the expected reward of BTC. Table 4 shows that a 1% increase in the BTC’s expected reward decreases the hash rate of BCH by 3.98% and BSV by 3.19%, and so on. Thus, it shows that the PoW currencies of the same hash algorithm are interconnected through the mining market.

image

3 Likes
#5

And a hash market it is :slight_smile: Which is why I think survival of all SHA-256 coins is in the best interest of miners, because each has the potential to increase total addressable hash market. It doesn’t pay to play favorites. Hashrate allocation across coins is a matter of simple economic calculation, and hardware ROI comes from total value of SHA-256 rewards. Therefore, if market success is not a 0-sum game then it makes sense to protect even minority coins, sometimes at a cost (sub-optimal mining, doesn’t necessarily mean mining at a loss).

This is also why I think it’s safer to be a minority SHA-256 coin than to roll out some new algorithm for which there are no specialized miners and no developed market, because every minority SHA-256 benefits from the “reserve” power ready to step in and protect against any rented hashrate or botnet attack.

Javier Gonzales believes that hashrate could be used to make governance decisions. This is something I disagree with, because miners have no incentive to get directly involved unless the coin is under hashrate attack or there is threat of changing the mining algo or breaking mining hardware in other ways (like block header changes). However, he did good to collect on-chain evidence of miners getting involved in those cases where survival was at stake: Executive Hashpower.

Btw, his “Bitcoin Mining Parliament” chat looks cool, even though I don’t expect it to become popular.

It would be cool to hear your thoughts on the topic!

PS Here’s another useful reference dispelling some myths of relationship between PoW mining and energy use: Blockchain Energy Use: A Media Package

2 Likes
#6

We kind of agree with this. In the paper, we pointed out that BTC’s sticking to the original DAA destabilizes the SHA-256 mining market. However, because some miners can benefit from the unstable market by swing mining, they will have little incentive to change this (my coauthor discussed this issue in another paper Noda, Okumura, and Hashimoto, 2020).
An Economic Analysis of Difficulty Adjustment Algorithms in Proof-of-Work Blockchain Systems by Shunya Noda, Kyohei Okumura, Yoshinori Hashimoto :: SSRN

2 Likes
#7

Yes that definitely answered q2. Thank you for that. I still wasn’t able to understand the logic related to q1. I am suggesting that it is an unsupported logical leap to suggest that miners per se are loyal rather than aggregate hashrate. In my understanding, miners are generally miners of all sha256 chains because the vast amount of hashrate does not operate independently. It operates through sophisticated pools (either 3rd party or internal to a company) which balance according to prices and other criteria across available sha256 chains. You may have countered that and I just wasn’t able to understand the logic.

#8

I got you point. You mean that the empirical analysis is all about the aggregate behavior of the miners and the statement about the individual miners are just conjecture. This is also what we meant but our writing was not great. To infer the behavior of individual miners from the aggregate behavior of miners, we need to incorporate the micro structure such as the mining pools, the thickness of the exchange market, and so on, into the analysis. We will try to speak to these points in the future research.

2 Likes
#9

Yes. It’s a point where your research intersects with political issues so it may get additional attention. Thanks for discussing it.

#10

Thinking about this again, I wonder if there is some way to consider that the fact of original DAA itself might influence the stickiness of aggregate hash supply? In other words, a rational pool that wants BTC to thrive would know that allowing hashrate to decrease during a given DAA period has a high chance of leading to a negative chain of events - increasing block competition, increasing fees, and potential fallout from that such as loss of users to alternative goods. There is a graph around somewhere that suggests users sought alternative goods when block competition was high in 2018.

#11

It is theoretically possible, but not easy to empirically test. We will need information on the mining pool level hash supply. Based on that, we can measure how far their hash response is from the “optimal” hash supply to maximize the instant profit. From that pattern, we may be able to learn some alternative incentives for the mining pools other than the instant profit. It is an analysis similar to the detection of collusion in Economics.

2 Likes
#12

Thanks for sharing that. It sounds interesting. Another potential sign would be changes of behavior in the blocks leading up to a DAA change where incentives start to include not only current incentive but future as well.