Research: Block difficulty as a price oracle

bitcoincashautist · December 13, 2024, 5:04pm

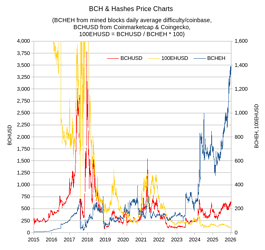
I had a hypothesis that difficulty could be used to estimate the price of BCH in MWh, which I spent some time researching, and here I will share my findings.

First, recall that:

Block headers encode a 4-byte compressed_target which is a custom scientific notation: {3 byte mantissa}{1 byte exponent} where we obtain the int256 target by doing: mantissa * 2^((exponent - 3) * 8);
To be accepted by the network, block header hash must satisfy block_hash <= target;
Chainwork contribution is the expected number of hashes given by 2^256 / (target + 1), and cumulative chainwork is used to resolve which is the “longest” chain;
max_target is that of genesis block, which had compressed_target = 0xffff001d and is the easiest PoW;
Difficulty is defined as target / max_target;
Difficulty of 1 is then equivalent to chainwork of 4295032833, which is equal to 4.29 gigahashes.

We can think of hashes as a commodity extracted by the miners and then sold to blockchain network(s) in exchange for block reward.
We postulate that each block is a price point, where the full block reward (subsidy + fees) is exchanged for the hashes. The network is the buyer, and miners are the sellers.
If miners are over-producing, the DAA auto-corrects the purchase price by slowing down the blocks, and if they’re under-producing, the DAA auto-corrects the purchase price by speeding up the blocks. The DAA functions as an automatic market maker (AMM).

If that is so, we can define BCHGH price as (difficulty / (subsidy + fees)). Each block header & coinbase TX is then a native price oracle for BCHGH. We don’t need any external data in order to know this price, the blockchain itself records it.

But can we somehow link hashes to something in the real world? It is impossible to produce a hash without spending energy, so if we know the average amount of energy used to produce a hash then we could have some estimate. But the amount of energy changes with each new generation of ASICs.

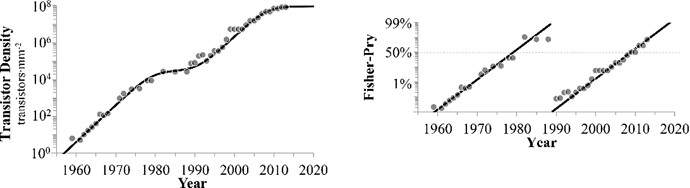
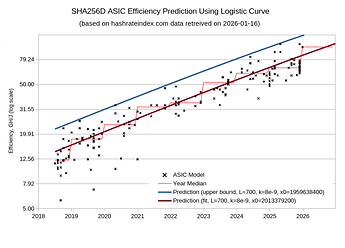
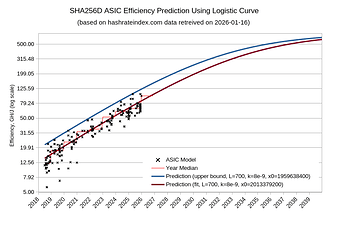
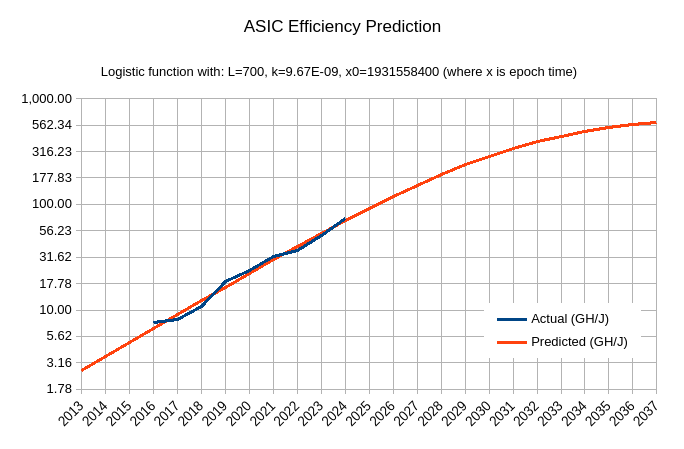
Thankfully, it looks like we can model the efficiency gains using the Logistic function. I fit one such curve on the data (source, fetched on 2024-11-08) and got:

asic_efficiency = 700 / (1 + e^(-9.67E-09 * (x - 1931558400)) (unit: GH/J)

where:

x is epoch time
numerator 700 sets the asymptote, roughly corresponding to 0.5nm tech (further 10x improvement from current 5nm tech)
factor of 9.67E-09 found such that the curve angle on log scale matches the angle of data points
offset 1931558400 to fit the data points

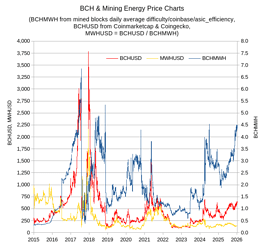
With this, we can infer BCHMWH price using (difficulty / asic_efficiency) / (subsidy + fees).

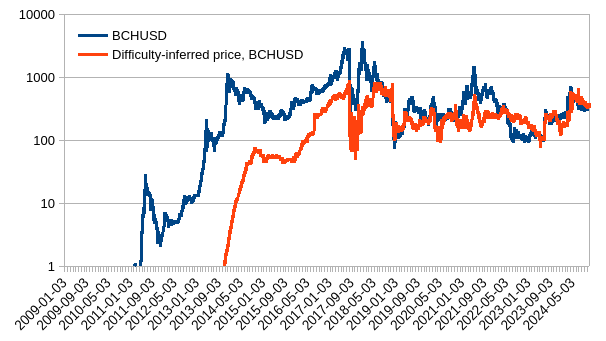
Then, to better see whether this would map to external prices I pulled FRED global energy price index ($100/MWh in 2016) and then obtained inferred BCHUSD.

Let’s see how so inferred price matches real prices (coinmarketcap), for both BTC and BCH.

BCHUSD	BTCUSD

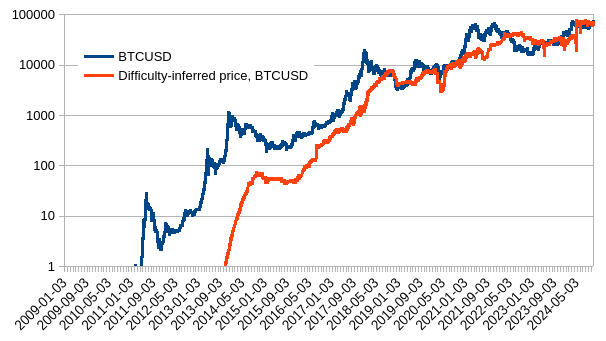Not perfect, not bad. Before 2015, the mining market and ASIC development was still immature but value of block reward was enough to crowdfund rapid catching up with state of the art chip-making. Since it caught up, we can observe better correlation between inferred and actual.

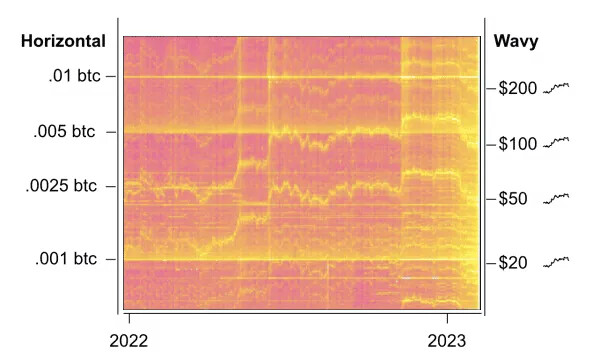
Use of difficulty price oracle for minimum relay fee algorithm

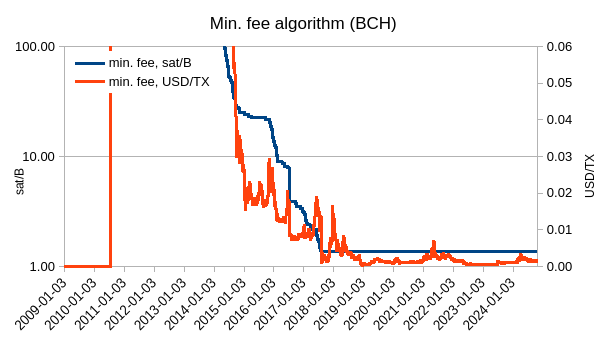
What I really wanted to see is whether we could use difficulty to automatically set the minimum relay when new price highs are reached, in order to minimize the lag between price making highs and people coordinating a reduction of min. fee.

To not have to depend on external data, the idea to set the min. fee in watt-hours rather than sats or USD, and just use the ATH of BCHMWH to set the min. fee in sats.

Here’s how that would look like for 0.1 Wh/byte

BCH	BTC

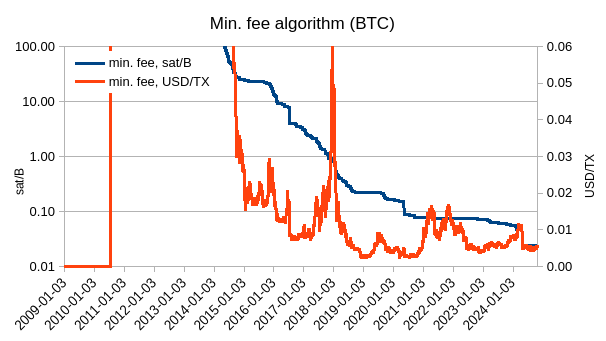As we can see, setting it so would keep the min. fee under $0.01. BCH would have it lower because current price is about 10% of last ATH, while BTC is near its ATH.

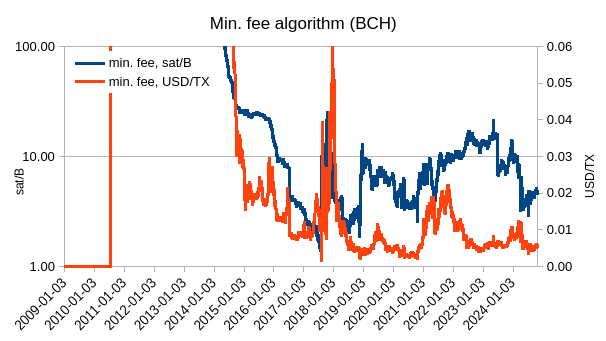
If we would not use ATH price but current price, then the min. fee would not only be going down with new ATHs but it would be freely floating and would look like this:

BCH	BTC

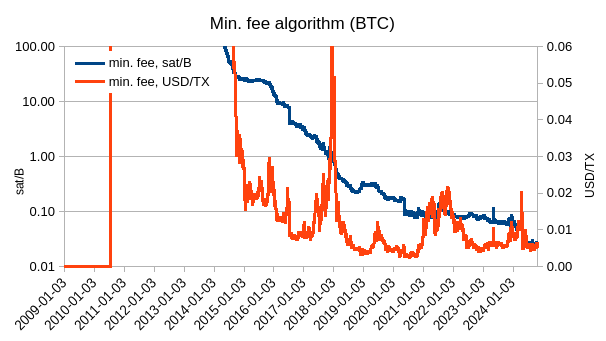Acknowledgements

To @Licho for his work (“Proportional block reward as a price stabilization mechanism for peer-to-peer electronic cash system”) that inspired this work.

Kilian · November 15, 2024, 10:25am

My first question is about the current DAA , for finding the compressed_target in the block header the exponent is deducted by 3, i’m assuming this is just so the value can be negative or positive without the need of a sign bit?

Secondly why do you chose this specific curve to fit the data and choose the asymptote at 700?

bitcoincashautist · November 15, 2024, 9:31pm

This is not a feature of current DAA but of block header format, as decided by Satoshi. Exponent of 0 “erases” whatever 3 bytes of mantissa by shifting them right and then target is 0.

Moore’s law is pure exponential, which is why it will eventually be broken, because in nature many things start off as exponential, but nothing can be exponential forever, because there are phyical limits to everything.

Logistic function models a process where the exponent decays with time, like in population growth. See Logistic function - Wikipedia

700 is a nice round number roughly 10x from where we are now with 5nm tech, and just a guess that efficiency gains will almost fully diminish at about 0.5nm (reminder that diameter of smallest atom, hydrogen, is 0.1nm, and diameter of Si is 0.2nm, and you need more than 1 atom to make a gate).

Btw, look what I found now: David Burg, Jesse H. Ausubel, “Moore’s Law revisited through Intel chip density”

They found that the data fits to 2 Logistic curves:

Sigmoidal trends of processor evolution

The density of transistors was then fit to Eq (2), resulting in a well-defined bi-logistic trend (Fig 4A). Interestingly, both phases have characteristic times (Δ t i ) of 9.5 years. Midpoints of these distinct growth curves occurred circa 1979 and 2008, with approximately 30 years separating them.

So, who knows, maybe ASICs will saturate as predicted, but then a new paradigm will be discovered and kick-off a new Logistic curve.

Kilian · November 16, 2024, 12:33am

Thanks, woops I was totally misinterpreting that first part, its just how the difficulty number is represented.

Using a logistic function intuitively makes total sense in a situation like this. The method of approximating where the efficiency gains hit a limit is the hard part. It sounds quite reasonable to assume the gains diminish at the atom level.

Jonathan_Silverblood · November 17, 2024, 9:44am

slightly off topic, but now I imagine us discovering a blockspace broadcasted through space, we measure the hashes and determine that whatever civilization produced that blockchain must have had access to some X amount of energy, setting a lowest indicator for their location on the Kardashev scale, effectively telling us that we’re in the Dark Forest and should be really really careful about what we do next -.-

A bit more on-topic - this is interesting. I’m not sure if the slight discrepency in the USD cost you predict with this VS the market price is due to enefficiency in the model or the market, to be honest. It’s probably a bit of both. Either way, to use the data point in a contract we would need to either support introspection of the blockchain / headers, or a contract that validates the block headers and outputs the price points as tokens. would be interesting to see if such a contract could also automate the token ditribution through AMM and let the market determine the price of this data.

bitcoincashautist · November 18, 2024, 12:03pm

It needs a guess on efficiency of their hardware. It could still be a measure of how more advanced than us they are - but we couldn’t tell whether it is due to 100x more efficient hardware or due to 100x more energy spent - likely due to both.

Of course there’d be discrepancy, because in reality ASICs don’t magically and smoothly get replaced for latest model and with 0 costs. Also, miner’s average energy cost is not equal to world average energy cost.
What’s interesting is that there’s not so much discrepancy from 2018 onwards - possibly because in a developed market Logistic curve models ASIC saturation, too.

That’s what got me here, I want to have an on-chain header oracle so we can trustlessly speculate on GH/s and on GH/BCH, and have a GH overcollateralized stablecoin.

I have a work-in-progress oracle design that validates block headers and emits verified state as tokens, but unfortunately I can’t reliably extract total fees because that’d require parsing coinbase transactions, too, and if they’d be too big then they’d be impossible to parse due to VM limits.

Possible solutions:

introspection of blockchain headers (& some aggregate data like total fees collected)
streaming hash opcodes (so you could perform hash of a big message by splitting the job to multiple chained TXs)
different limits for coinbase and other TXs, so that coinbase can reliably fit inside some non-coinbase TXs unlocking bytecode

Kilian · November 18, 2024, 12:47pm

I once purposefully bought some old secondhand ASIC’s that in no way could ever mine profitably in my area due to a high price per KWh. But by placing them in my basement I was able to offset some of my heating bill because I didn’t have to heat the floor above as much anymore.

Even though the actual price per hash was higher in this case the fact that is was still online providing hash power was because in this case the heat produced was also perceived as value and part of the equation for the AMM.

Aside from this niche use case I would expect the model to become more accurate over time.

2qx · November 22, 2024, 5:59pm

It should be possible to create a permissionless oracle from this by passing the next header to a contract and having the timestamp and target written to an NFT commitment.

There would have to be a method to step backward in case of a reorg.

hash (32 bytes), time (4 bytes), target (4 bytes),

pragma cashscript ~0.11.0;
    
contract TargetOracleVault() {

    // nftCommitment
    // hash (32 bytes), time (4 bytes), target (4 bytes)

    // block Header Format
    // https://reference.cash/protocol/blockchain/block/block-header
    // version (4), prev_hash (32), merkle root (32), time (4), target (4), nonce (4)

    // Require recipient's signature to match
    function step(bytes header){

        // require the NFT token is returned
        require(this.activeInputIndex == 0);
        require(tx.inputs[this.activeInputIndex].lockingBytecode == tx.outputs[this.activeInputIndex].lockingBytecode);
        require(tx.inputs[this.activeInputIndex].tokenCategory == tx.outputs[this.activeInputIndex].tokenCategory);

        // verify the previous header hash matches the incoming oracle commitment
        require(
            tx.inputs[this.activeInputIndex].nftCommitment.split(32)[0]
            == 
            header.split(4)[1].split(32)[0]
        );
        bytes timeTarget = bytes(header.split(68)[1].split(8)[0]);
        // update commitment
        // push new hash + time/target
        require(
            tx.outputs[this.activeInputIndex].nftCommitment 
            == 
            hash256(header) + timeTarget
            );
    }
    function step_back(){
        // TODO: converse of step
        require(true);
    }

    function use(){
        // let the oracle be used by anyone returning the NFT to the contract
        require(
            tx.outputs[this.activeInputIndex].lockingBytecode 
            == tx.inputs[this.activeInputIndex].lockingBytecode
            );
        require(
            tx.inputs[this.activeInputIndex].tokenCategory  
            == tx.outputs[this.activeInputIndex].tokenCategory
            );
    }
}

Or something like that.

bitcoincashautist · November 22, 2024, 7:13pm

That’s exactly what I’ve been working on. Here’s the WIP in Bitauth IDE.

Idea is to have 3 contracts:

funder: simply collects money that can be used to pay fees for the builder contract
builder: parses a header and updates oracle NFT state, every epoch end, builder emits a copy of its NFT to the replicator contract
replicator: emits immutable copies for consumption by users - the replicator fee goes to funder contract

The builder verifies PoW target against block header hash, verifies DAA updating, and timestamp > MTP, so in order to fool the oracle someone would have to spend real PoW.

There is no reorg support, rather, I allow the oracle to fork freely: each update creates 2 outputs: new state + copy of the old sate (what I call a “bud”) that can be uses to extend an alternative tip. These buds eventually expire and get cleaned up.

I store height + H(H(firstState) + H(lastState)) in the NFT commitment, where each state consists of: headerHash, height, timestamp, daaTimestamp, daaBits, cumulativeChainwork, mtpState.

Once builder reaches epoch end, it resets to firstState=lastState and emits a replicator with the ending state. DAA epoch is 2 weeks and my idea was to have builder epoch be 1 week, so it would align with BTC’s DAA updates every 2nd builder’s epoch. (I also have a BCH version that implemented ASERT verification).

Because NFT stores both firstState and lastState, user contracts can accumulate a bunch of NFTs, verify they link up, and sum the chainwork to prove as much PoW as needed for satisfactory security.

I kinda left it at that, but I want to to improve the funding cycle, if funder contract accumulates too much I’d like to have the excess funds sent to “security budget fund” contract that would drip the money to miners.

I focused on making an oracle for BTC headers, because then we could invite miners over to BCH to bet on BTC’s DAA updates: how many hashes will be generated by BTC network between now and 7d from now? The oracle would provide the number, and the number can settle a hedge contract. If price of BTC goes up between open & close, there will be more hashes generated, and if price of BTC goes down, there will be less.

BitcoinCashPodcast · November 22, 2024, 11:04pm

This is incredibly good work. I am still digesting and thinking about this.

Intuitively to me a floating min-fee algorithm similar to ABLA would be awesome. A “one way only” algorithm just doesn’t have the same elegance intuitively, but maybe with thought I’ll see how it would be better.