TL;DR: it is a perfect DAA, and I want to share some insights about it here, and gather whatever other materials about it in this one place.
As part of my work on faster blocks CHIP, I had to study ASERT in order to adapt it to changeable target block time. There I really appreciated its mathematical elegance which made it easy to tweak while maintaining all of its nice properties.
Mathematical Analysis
Recall the “absolute” version:
target_{n+1} = targetAtActivation * 2^((timestamp_n - targetTimestamp) / tau) ,
where targetTimestamp_{n+1} = (n + 1 - n_activation) * targetBlockInterval .
From there, we can simply calculate relative (block-to-block) adjustment by dividing some block’s difficulty with the difficulty of block before:
target_{n+2} / target_{n+1} = (targetAtActivation * 2^((timestamp_{n+1} - targetTimestamp_{n+2}) / tau)) / (targetAtActivation * 2^((timestamp_n - targetTimestamp_{n+1}) / tau)) .
The constants cancel each other out, the 2 timestamps reduce to solvetime, and 2 targetTimestamps reduce to targetBlockInterval, and we get:
target_{n+2} / target_{n+1} = 2^((solvetime - targetBlockInterval) / tau) ,
or what zawy called the “relative” version.
Mathematically speaking, the “relative” is the finite difference derivative of the “absolute”.
Or, looking at it from the other direction, the “absolute” is the closed form solution to the ordinary differential equation defined by the “relative” expression.
When you use the “absolute” expression, you’re simply plugging in timestamps into the closed form expression.
When you use the “relative” expression, you’re actually performing numerical integration.
In fields like physics, we discover the differential equation governing some natural process (“How does this change with x?”), but here we actually choose the differential equation (“How do we want this to change with x?”) governing the system.
“Relative” and “absolute” ASERT are not different algorithms, they’re the same mathematical object viewed through integration vs differentiation.
Similarly, the WTEMA is also an ordinary differential equation (ODE):
target_{n+2} / target_{n+1} = 1 + (solvetime - targetBlockInterval) / tau ,
but this ODE is inherently path-dependent, so no closed form solution exists.
Comparing the two ODEs:
| Property | Linear form (WTEMA) | Exponential form (“relative” ASERT) |
|---|---|---|
| Log-domain behavior | Nonlinear | Linear |
| Closed-form sum | No | Yes |
| Multiplicative consistency | No | Yes |
| Path independence | No | Yes (depends only on total time and block count) |
ASERT’s ODE makes log-target a simple accumulator of timing errors, which is exactly what lets the absolute form exist, and what you want for a difficulty adjustment algorithm.
Multiplicative consistency practically means that in ASERT, a 5-min block will perfectly cancel a 15-min block: difficulty before and after the two blocks will be exactly the same. In WTEMA, this is not the case: a fast block followed by an equally slow block leaves difficulty slightly higher than before, causing systematic drift under volatility.
@jtoomim did great work on ASERT, and I have re-read his analysis and explanation (BCH upgrade proposal: Use ASERT as the new DAA, July 2020) many times.
Few months after activation, @freetrader did some before-after analysis: ASERT: Before and After
Bitcoin Cash (BCH) activated ASERT back in 2020, and it has since performed great. There’s even been academic research (Kawaguchi, Kohei and Komiyama, Junpei and Noda, Shunya, Miners’ Reward Elasticity and Stability of Competing Proof-of-Work Cryptocurrencies (August 27, 2022)) praising it:
Abstract
Proof-of-Work cryptocurrencies employ miners to sustain the system through algorithmic reward adjustments. We develop a stochastic model of the multicurrency mining market and identify conditions for stable transaction speeds. Bitcoin’s algorithm requires hash supply elasticity < 1 for stability, while ASERT remains stable for any elasticity and can be interpreted as a form of stochastic gradient descent under a certain loss function. Interactions with other currencies can relax Bitcoin’s stability requirements. Using a halving event, we estimate miners’ hash supply elasticity and conduct counterfactual simulations. Our findings reveal Bitcoin’s heavy reliance on low hash supply elasticity and interactions with smaller cryptocurrencies, suggesting an algorithm upgrade is crucial for stability.
and the authors (@kkawaguchi) were so kind to share their work and spend some time discussing it on this forum.
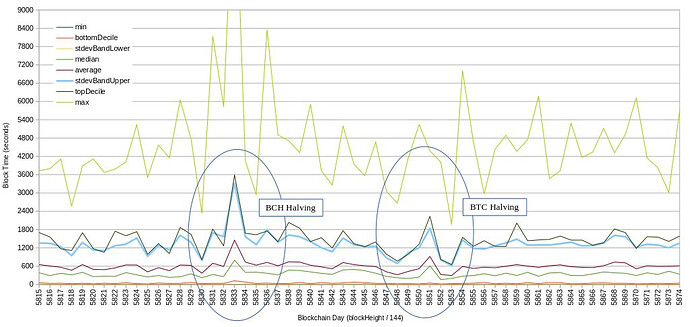
Later, I did some analysis of our first halving with ASERT-DAA: Lets talk about block time - #65 by bitcoincashautist
Around that same time @tom was asking about whether the same deviation from 10-min target will always cause the same difficulty change %-wise, to which the answer is a definite YES. This was the first time I derived it myself and understood mathematical elegance of it.
zawy12, known for his independent research into difficulty adjustment algorithms, has written at length about it.
I think this covers it well. I’ll remember to add more to this thread if I find or remember more resources, analyses, etc.