I would encourage everyone in this discussion to look at TailStorm being discussed here: Tailstorm: A Secure and Fair Blockchain for Cash Transactions - #2 by _minisatoshi
All the benefits + more of shorter block times, without the drawbacks.

I would encourage everyone in this discussion to look at TailStorm being discussed here: Tailstorm: A Secure and Fair Blockchain for Cash Transactions - #2 by _minisatoshi
All the benefits + more of shorter block times, without the drawbacks.
With a random process like PoW mining is, there’s a 14% chance you’ll have to wait more than 2 times the target (Poisson distribution) in order to get that 1-conf.
This is not really correct. It’s much worse than that: 40.6%. Russell O’Connor discusses this here.
The 14% is the probability that the time difference between two blocks is longer than 20 minutes. (The time between blocks has an exponential distribution with rate parameter 1/10 minutes).
That is not the probability that a user waits longer than 20 minutes for their first confirmation. A user is not equally likely to broadcast a transaction during a long block time and a short block time. They are much more likely to broadcast during a long block time because long block times cover longer periods. (We assume that transactions are confirmed in the next mined block and that the timing of a broadcast transaction and the timing of a block being mined are independent.)
The probability distribution of a user’s wait time to first confirmation is an Erlang distribution with shape parameter 2 and rate parameter 1/10 minutes. This is the same as a gamma distribution with shape parameter 2 and rate parameter 1/10 minutes.
This statement is also not correct: “With 2-minute blocks, however, there’d be only a 0.2% chance of having to wait more than 12 minutes for 1-conf!” The correct probability is about 1.7%. You can get this probability by inputting this statement in R: pgamma(12, shape = 2, rate = 1/2, lower.tail = FALSE).
IMHO, O’Connor’s explanation isn’t very detailed, but you can convince yourself that the user’s wait time is an Erlang(2, 1/10) distribution with a simulation. In R it would be:
set.seed(314)
exp_draws <- rexp(1e+07, rate = 1/10)
# Draw ten million block inter-arrival times
user_wait_index <- sample(length(exp_draws), size = 1e+06, replace = TRUE, prob = exp_draws)
# Draw one million indexes from the exp_draws vector. prob = exp_draws means
# that the probability of selecting each index is proportional to the inter-arrival time.
user_waits <- exp_draws[user_wait_index]
# Create the user_waits vector by selecting the appropriate exp_draws elements
prop.table(table(user_waits >= 20))
# The proportion of user_waits that are longer than 20 minutes:
# FALSE TRUE
# 0.593514 0.406486
ks.test(user_waits, pgamma, shape = 2, rate = 1/10)
# Kolmogorov-Smirnov test fails to reject the null hypothesis that the
# user_waits empirical distribution is the same as a gamma(2, 1/10) (i.e. Erlang(2, 1/10))
# Asymptotic one-sample Kolmogorov-Smirnov test
# data: user_waits
# D = 0.00074215, p-value = 0.6404
# alternative hypothesis: two-sided
# Make a histogram of user_waits and compare it to the
# probability density function of gamma(2, 1/10)
hist(user_waits, breaks = 200, probability = TRUE)
lines(seq(0, max(user_waits), by = 0.01),
dgamma(seq(0, max(user_waits), by = 0.01), shape = 2, rate = 1/10),
col = "red")
legend("topright", legend = c("Histogram", "PDF of gamma(2, 1/10)"),
lty = 1, col = c("black", "red"))
I’m not 100% sure about this, but I think your table also is incorrect. Let x be the number of confirmations and y be the average block time. We use the Erlang distribution again because the shape parameter is the number of events that we are waiting to occur. We add 1 to the shape parameter to factor in the probability that the user broadcasted their transaction during an “unluckily” long block time interval (similar reasoning as before). The distribution of the waiting time would be Erlang(x + 1, 1/y).
When the user is “expecting” a certain number of confirmations in 60 minutes, it would be 6 with the current 10 minute block time and 30 with a 2 minute block time. The distribution of waiting times for a user waiting for 6 blocks with a 10 minute average block time would be Erlang(6 + 1, 1/10). For 30 blocks with a 2 minute block time it would be Erlang(30 + 1, 1/2).
If my conjecture is correct, to fill in the table you would input pgamma(c(70, 80, 90, 100), shape = 6 + 1, rate = 1/10, lower.tail = FALSE) in R for the first column and pgamma(c(70, 80, 90, 100), shape = 30 + 1, rate = 1/2, lower.tail = FALSE). That would give you:
| expected to wait | actually having to wait more than | probability with 10-minute blocks | probability with 2-minute blocks |
|---|---|---|---|
| 60 | 70 | 45.0% | 22.7% |
| 60 | 80 | 31.3% | 6.2% |
| 60 | 90 | 20.7% | 1.2% |
| 60 | 100 | 13.0% | 0.16% |
For reference, I simply used the spreadsheet Poisson function to calculate my numbers:
=1-POISSON(0,time/target_time,0)
Which calculates inverse of observing exactly 0 occurences during the time I expect to see time/target_time occurrences.
Oh I see, my numbers are really numbers of blocks longer than X, but from individual user PoV when he randomly decides to make a TX he can land anywhere between 2 occurrences with duration X between them and because longer durations are well, longer, they take a bigger % of the timeline, so there’s a higher probability of landing in one of the longer ones, and so from user PoV the probability of wait will be different so we need to use Erlang rather than Poisson. Got it. And wow, it’s even worse than I thought. 
Thanks for the peer review!
PS I reproduced the above numbers using LibreOffice Calc spreadsheet function GAMMA.DIST:
For the 6-conf wait time >70min probability is: =1-GAMMA.DIST(70, 7, 10, 1) with 10-min blocks.
For 1-conf wait time >20min probability is: =1-GAMMA.DIST(20, 2, 10, 1) with 10-min blocks.
So, Poisson distribution gives us a birds eye view of block times by answering the question: “What % of N block intervals will be longer than X minutes.”
But that’s not answering the question I wanted to ask: “If I make a TX, what are the odds I’ll have to wait more than X minutes for N confirmations.”
As explained above by @Rucknium, the Erlang / gamma distribution answers that.
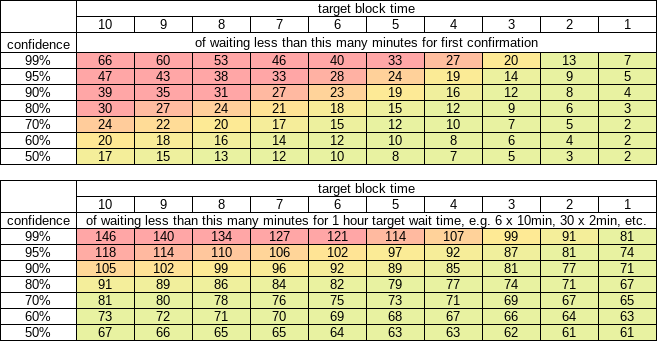
And it looks like 50% chance of having to wait longer than 17 minutes, and 19.9% chance for longer than 30 minutes, wow! We’d need 6 minute target if we wanted 50% chance of <10min.
Put another way, with 10 minute target you can have only 50% confidence you’ll get that 1 confirmation before 17 minutes passes.
Further and further we go towards why TailStorm is so promising.
Moving my reply here to keep on-topic:
I’ll take the opportunity to share the historical ideas on this.
Zero conf is (and always used to be) secure enough for most. It is a risk level that most merchants will be confident with up until maybe $10000. Heavily dependent on the actual price of a unit and the cost of mining a single block (wrt miner assisted ds).
This is like insurance. Historical losses decide the risk profile. Which means, the better we do with merchants not losing money due to double spends, the higher the limit becomes for safe zero-conf payments.
As such, in a world where Bitcoin Cash is actually used for payments the situation you refer to as “requiring a confirmation or more” tends to be the type that doesn’t really care about block time.
They are the situations where you’re giving your personal details and do a bank transfer. They are the situations where you order it online and it will not be delivered today anyway. These are the situations where, in simple words, the difference between 10 minutes and 2 hours confirmations are completely irrelevant.
I don’t disagree at all about the security of 0-conf. Not one bit. Doesn’t mean that we should completely stay away from improving the confirmation experience to impact real world users and situations for the foreseeable future. Not to mention the other benefits.
Nobody disagrees it would be nice. But the cost is outlandish. Would you buy a $500 pair of jeans for a kid that will outgrow them in a year. What about somene buying a $5000 bicycle just to cover the year until it becomes legal to drive?
This is the disconnect that really gets me…
When do you think any such changes are possible to become used by actual people? A TailStorm will take several years before it can be deployed, another couple before it is used by companies (if ever). Reminder that SegWit usage took 7 years to become the majority used address type.
So, you’re advocating ideas that are intermediary, but can’t possibly be in the hands of users in less than 5 years… See how that is a contradiction?
I’m not stopping you, I’m just realistic about what can be done and what gives the best return on investment.
But it has come to the point that it needs to be clarified that this series of ideas is mostly just harmful for BCH at this point. If it stayed on this site it wouldn’t be harmful, but a premature idea that nobody endorses is being pushed in the main telegram channels daily, is pushed on reddit and on 𝕏. The general public thinks this is happening. While not a single stakeholder is actually buying into this.
Hell, there isn’t even any actual reason given for this shortening that stands up to scrutiny.
That is mostly on @bitcoincashauthist, but you both are not listening to stakeholders and just marching on. Again, if its just here, that’s no problem. It is the going to end-user locations with this that is giving a completely different impression.
Tailstorm would offer benefits immediately upon activation, depending on implementation it can immediately:
Based on my research I think there are 3 ways (edit: 4 actually) to improve confirmation time:
| effect | plain block time reduction | plain subblocks | “inner” Tailstorm | “outer” Tailstorm |
|---|---|---|---|---|
| Reduced target wait time variance (e.g. for 10 or 60 min. target wait) | Y | Y | Y | Y |
| Increased TX confirmation granularity | 1-2 minutes | Opt-in, 1-2 minutes | Opt-in, 10-20s | 10-20s |
| Requires services to increase confirmation requirements to maintain same security | Y | N | N | Y |
| Legacy SPV security | full | 1/K | 1/K | near full |
| Breaks legacy SPV height estimation | Y | N | N | Y |
| Increases legacy SPV overheads (headers) | Y | N | N | Y |
| Selective opt-in “aux PoW” SPV security | N | Y | Y | N |
| Breaks header-first mining every Kth (sub)block | N | Y | Y | Y |
| Additional merkle tree hashing | N | Y, minimal if we’d break CTOR for summary blocks | Y, minimal if we’d break CTOR for summary blocks | minimal |
| Increased orphan rate | Y | Y | N | N |
| Reduces selfish mining and block witholding | N | N | Y | Y |
I could say the same: pretending there’s no confirmation time problem is harmful for BCH.
I can accept this criticism, we’re not yet in the stage where we could hype anything as a solution.
These two tables should be sufficient reason, unless you will hand-wave the need to ever wait for any confirmations.
Table - likelihood of first confirmation wait time exceeding N minutes
Table - likelihood of 1 hour target wait time exceeding N minutes
This is a great summary – thank you.
Might be helpful to tag this consolidated reply back to the TailStorm chain too.
I made a schematic to better illustrate this idea, it would be just like speeding up blocks, but in a way that doesn’t break legacy SPV:
It would preserve legacy links (header pointers) & merkle tree coverage of all TXs in the epoch.
This doesn’t break SPV at all, it’d be just as if price did 1/K and some hash left the chain.
Legacy SPV clients would continue to work fine (at reduced security) with just the legacy headers.
However they could be upgraded to fetch and verify the aux PoW proofs just for most recent blocks, to prove that the whole chain is being actively mined with full hash.
So, the increased overheads drawback of just accelerating the chain would be mitigated by this approach, too.
ok, now your only advantage left is to have more consistent block-times, what about not having all this tailstorm and all this complexity but just allow a more advanced p2peer way of mining.
Specifically I’m thinking that a p2peer setup may be extended to be cumulative.
P2Peer is today a mining standard that fits in the current consensus rules and allows miners with a partial proof-of-work to update the to-be-mined block with a new distribution of the rewards and such.
Where it differs with your suggested approach is that, simply said, you lower the number to throw on a 20-sided dice to be 16 instead of 20, but you requires a lot more of them to compensate.
This is the simple and conceptual difference that you claim is the reason that tailstorm has more consistent blocktimes.
My point is, if that is your argument you should dress it down and make those 20 (or whatever number) of block-headers be shipped in the block and make the consensus update to allow that.
Minimum change, direct effect.
I dislike the soft-fork lying changes that say it is less of a change because it hides 90% of the changes from validating peers. That is a lie, plain and simple. It is why we reject segwit, it is why we prefer clean hard forks. As such, a simple and minimum version of what you propose (a list of proof of work instead of a single proof of work) is probably going to be much easier to get approved.
A simple list of 4 to 8 bytes per POW-item, one for each block-id that reached the partial required PoW, can be added in the beginning of the block (before the transactions) to have this information.
The block-header would stay identical, the difficulty, the merkle etc are all shared between POW items and the items themselves just cover the nonce and maybe the timestamp-offset. (offset, so a variable-size for that one)
The main downside here is that a pool changing the merkle-root loses any gained partial PoW, as such while confirmations may be much more consistent, the chance of getting into the next block drops and most transactions should expect to be in block+2.
Reasonably simple changes:

New block-header-extended:
This entire dataset is to be hashed to become the block-id which is used in the next block to chain blocks.
To verify one takes the final blockheader and hashes that to get the work. Then for each sub-work item in the list replace in the final block-header the nonce and the time. The time is to be replaced by taking the ‘start-of-mining’ timestamp and adding to that the offset. After that hash the new 80 bytes header to get the work and add this to the total work done.
Now, I’m not suggesting this approach. It is by far the best way to do what tailstorm is trying to do without all the downsides, but I still don’t think it is worth the cost. But that is my opinion.
I’m just saying that if you limit your upgrade to JUST this part of tailstorm, it will have a hugely improved chance of getting accepted.
That’d be the only immediate advantage. However, nodes could extend their API with subchain confirmations, so users who’d opt-in to read it could get more granularity. It’d be like opt-in faster blocks from userspace PoV.
This looking like a SF is just a natural consequence of it being non-breaking to non-node software. It would still be a hard fork because:
Just to make something clear, the above subchain idea is NOT Tailstorm. What really makes Tailstorm Tailstorm is allowing every Kth (sub)block to reference multiple parents + the consensus rules for the incentive & conflict-resolution scheme.
With the above subchain idea, it’s the same “longest chain wins, losers lose everything” race as now, it is still fully serial mining, orphans simply get discarded, no merging, no multiple subchains or parallel blocks.
Nice thing is that the above subchain idea is forward-compatible, and it could be later extended to become Tailstorm.
Sorry but all that looks like it would break way more things and for less benefits, but I’m not sure I understand your ideas right, let’s confirm.
First, a note on pool mining, just so we’re on the same page: When pools distribute the work, a lot of work will be based off same block template (it will get updated as new TXs come in, but work distributed between updates will commit to same TXs). Miners send back lower target wins as proof they’re not slacking off and they’re really grinding to find the real win, but such work can’t be accumulated to win a block, because someone must hit the real, full difficulty, win. Eventually 1 miner will get lucky and win it, and his reward will be redistributed to others. He could try cheat by skipping the pool and announcing his win by himself, but he can’t hide such practice for long, because the lesser PoWs serve the purpose of proving his hashrate, and if he doesn’t win blocks as expected based on his proven hash the pool would notice that he suspiciously has a lower win rate than expected.
Now, if I understand right, you’re proposing to have PoW be accumulated from these lesser target wins - but for that to work they’d all have to be based off same block template, else how would you later determine exactly which set of TXs the so accumulated PoW is confirming?
I think it would work to reduce variance only if all miners joined the same pool so they all work on the same block template so the work never resets, because each reset increases variance. Adding 1 TX resets the progress of lesser PoWs. Like, if you want less variance you’d have to spend maybe first 30 seconds to collect TXs, then lock it and mine for 10min while ignoring any new TXs.
Also, you’d lose the advantage of having subblock confirmations.
And the cost of implementing it would be a breaking change: from legacy SPV PoV, the difficulty target would have to be 1 because of:
SPV clients would have to be upgraded in order to see the extra stuff (sub nonces) and verify PoW, and that would add to their overheads, although the same trick I proposed above could be used to lighten those overheads: you just keep the last 100 blocks worth of this extra data, and keep the rest of header chain light.
yes, very good to avoid, in other words.
If you disagree then the onus of proof lies on you.
You understand right, and the tech spec I added in a later edit last night makes this clear. There is exactly one merkle-root.
You are wrong to say that in order to reduce variance ALL miners must join the same pool for the same reason the opposite of all miners being solo miners is not that there is exactly 1 pool.
Every pool added will already have the effect of reducing variance.
You can suggest that making it mandatory for all miners to join 1 pool is better, but then I’d have to retort with the good old saying that socialism is soo good, it has to be made mandatory.
In other words, don’t force 1 pool, but allow pools to benefit the chain AND the miner.
Actually, this is incorrect, SPV mining doesn’t derive the difficulty (and thus work) from the block-id. There is a specific field in the header for it. I linked the specification in my previous message if you want to check the details.
The details on how it does work is also in the original post. Apologies for editing it, which means you may not have seen the full message in the initial email notification.
Again, not promoting this personally. Just saying that this has the same effective gains as your much more involved system suggestions, without most of the downsides.
I still don’t think this is a good idea, even though the avoidance of subblocks and avoidance of changing difficulty and all the other things are useful, the balance is still not giving us enough benefit.
This led me to wrong conclusion on user experience, should’ve analyzed this better. It’s still Poisson for user wait times.
Yes, the length of the interval you land in will be based on Erlang distribution (20min average) but your average wait time until next block will still be 10min because when you make a TX you can land anywhere in the interval.
So: user wait time can be predicted with Poisson distribution, but the total duration of the block will be given by Erlang - which leads to impression that blocks are “always slow”, e.g. you pull up explorer it’s been 7 minutes since last block - and you will wait 10 more minutes: 17min total for the block but you only had to wait 10 minutes of that 17.
I made a little game to get the intuition for how random all of this is:
And yet… you click 11 times or more and you’ll see the percentiles table converge 
OK so initial search via both search engines and LLMs gave no results.
So I went to the source: Biggest mining pools of Feathercoin (1 min blocktime) and Dogecoin (1 min blocktime).
Feathercoin biggest pool:
Feathercoin smallest pool:
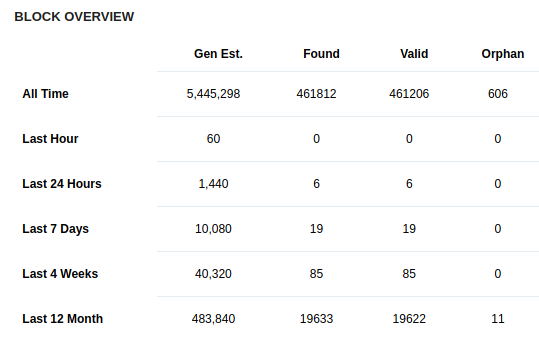
Dogecoin biggest pool:
Dogecoin small pool:
Additionally, there does not appear to be a difference between orphan rates for smaller and bigger pools.
ViaBTC has a nice stats page:
| Coin | ViaBTC Hashrate Share | ViaBTC Orphan Rate | Target Block Time, s |
|---|---|---|---|
| BTC | 11.4% | 0.03% | 600 |
| BCH | 20.8% | 0.02% | 600 |
| XEC | 39.1% | 0.06% | 600 |
| LTC | 28.5% | 0.02% | 150 |
| ETC | 1.6% | 0.23% | 15 1 |
| ZEC | 62.8% | 0.03% | 75 |
| ZEN | 52.1% | 0.1% | 150 |
| DASH | 29.2% | 0.05% | 150 |
| CKB | 10.9% | 3.39% | 10 2 |
| HNS | 62.4% | 0.01% | 600 |
| KAS | 12.9% | 0.63% | 0.1 3 |
| ALPH | 16.7% | 0.28% | 16 1 |
1 Orphans reduced with uncle block merging
2 Propose-commit transaction mining scheme propagates blocks with 0.5 * RTT, and adaptive block target time (bounded by 8 and 48 seconds) aims to maintain 2.5% average orphan rate (“NC-MAX”)
3 Orphans reduced due to BlockDAG structure (“GHOSTDAG”)
It is worth noting that once we do tests with 32MB (== 3.2MB with 1min blocktime) blocks with a testnet that spans over multiple continents, the orphan rate might fluctuate more.
Verifying the real-life functionality experimentally is the only way to achieve any sufficient level of certainty regarding this topic.